This is a continuation of (AES) The Advanced Encryption Standard [Part 1], so it is highly encouraged to read that post before reading this post. In that post, I gave the history of AES and also explained the internals of the AES algorithm.
In this post we will discuss these things:
- The AES key schedule
- Decryption of AES
- Security of AES
The Key Schedule of AES-128 bit Key
As stated in part 1, there are different version of AES. The difference in these versions is the size of the key, and an important thing to remember is the larger the key the more secure AES is. For this blog, I will only focus on the 128-bit key for simplicity. Note though that the key schedule differs slightly for each size, but I am confident if you understand how the 128-bit key schedule works, it will be easy for you to learn 192/256 on your own.
For AES-128 there are 11 subkeys which are derived from the 128-bit master key. You may wonder why there are 11 if AES-128 has 10 rounds, that is because before the 10 rounds you XOR the block with the first subkey. The 11 subkeys are stored in a key expansion array that splits up the 128-bit key into 4 32-bit words, in total after all 11 rounds there will be 44 words, denoted as W[0], W[1], …, W[43]. The key schedule is computed as shown in the diagram below:
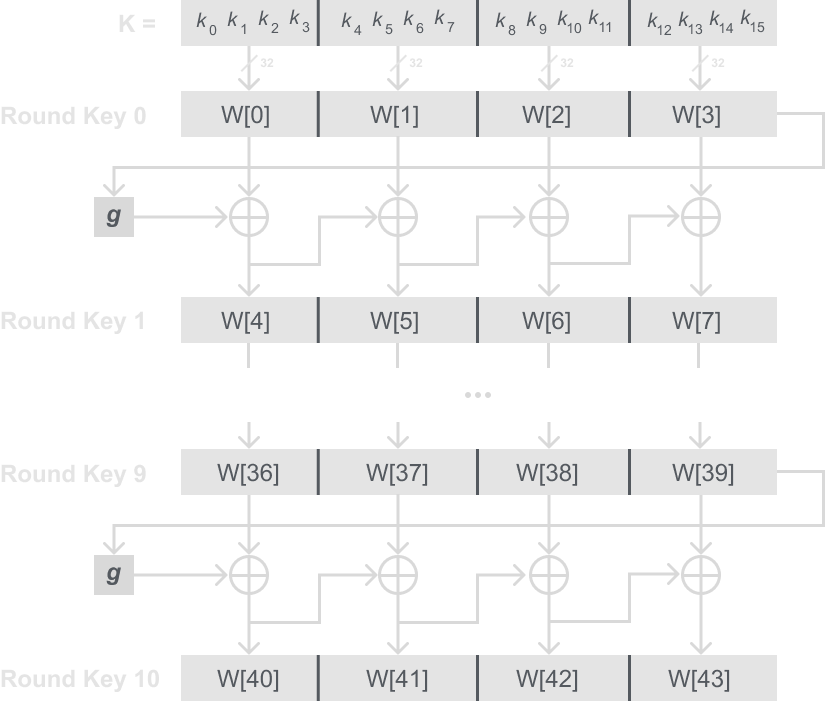
Key Schedule Mathematical Description
For those that need a bit more than a diagram, or prefer a formula to derive the key schedule is is quite easy to do that for AES-128.
For the left most word of a round key W[4i], where i = 1, … , 10 we can write:
W[4i] = W[4(i – 1)] + g(W[4i – 1]).
Here the function g() is a nonlinear function that takes four bytes as an input and gives four bytes as an output. The remaining 3 words of a round key are derived as such:
W[4i + j] = W[4i + j – 1] + W[4(i – 1) + j].
Where again i = 1, …, 10 and j = 1, 2, 3.
The g Function
All that is left is to understand what the g function is from our diagram and formula. Before I get into that, you will probably notice sources online that don’t show it this way, and instead just show the inner functions I will go into below. I simply did this so as to hopefully not overwhelm you at the very beginning.
The g function first rotates its four input bytes which we call RotWord, then performs the S-Box substitution just like in the AES algorithm which we call SubWord, and then adds a round coefficient RC to it which we call Rcon. The round coefficient is an element of GF(28), and note that it is only added to the leftmost byte of the word. The round coefficients also vary from round to round according to the table below:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| RCi | 01 | 02 | 04 | 08 | 10 | 20 | 40 | 80 | 1B | 36 |
So all that is left is to see how these are flow together, to see that here is a diagram of the g function below:
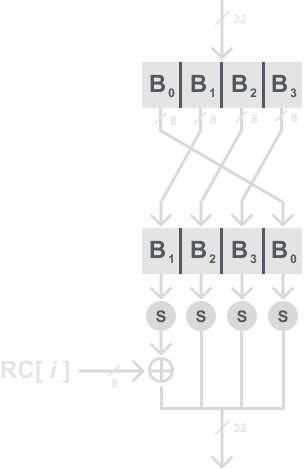
The g function serves two purposes. First, it adds nonlinearity to the key schedule. Second, it removes symmetry in AES. If you are familiar with the DES post, you will recall the importance of nonlinearity.
Decryption in AES
Unlike DES, the AES is not a Feistel network. Meaning we cannot just input our cipher text into out algorithm and get the decrypted plaintext outputted. Therefore we must actually invert all of the layers, i.e. the Byte Substitution now becomes Inv Byte Substitution, ShiftRows becomes Inv ShiftRows, and MixColumn becomes InvMixColumn.
Thankfully these functions are not too different from the original functions used in encryption. Note that also the order of the layers is inverted along with the order of the round keys. To see this see the diagram below:
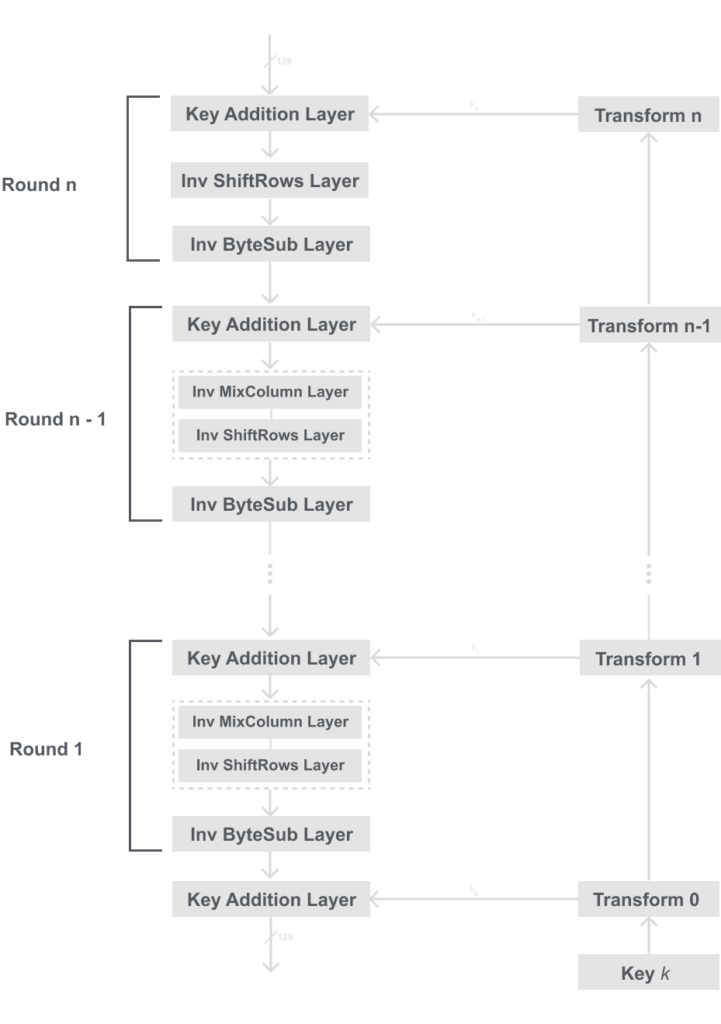
Now that we know the basic order of the inverse functions for decryption in AES, we will delve deeper and see what actually happens inside these layers. Recall that in AES we operate on bytes where 1 byte = 8 bits.
Below is a model for the inverse layers. You may notice it looks a lot like the one for encryption, and that because they are very similar. I suggest comparing them both and seeing how they differ and where they are the same. Below is the diagram for the internal inverse layers for AES:
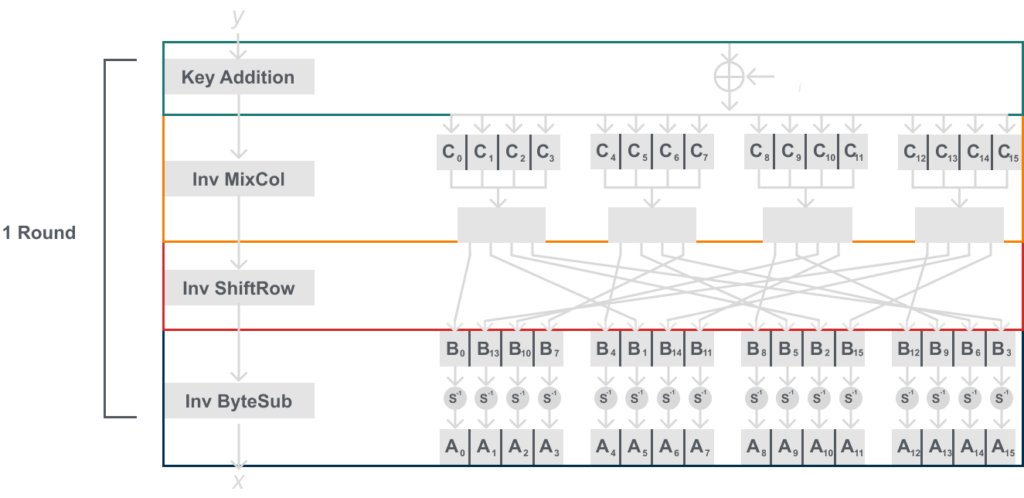
Recall that the XOR operation is itself its own inverse, thus the key addition layer does not have an inverse. You may also notice that we can’t reuse the same S-box, we need to use an inverse S-box.
This may seem like a lot, or too abstract for now. But just like with encryption I will into more depth on how the InvMixCol, InvShiftRow, and InvByteSub work.
Note that it is also best to think of the blocks of 16 bytes that are being decrypted to be arranged in a 4×4 byte matrix. You can see how we show the matrix below:

Inverse MixColumn
After the XOR operation in the Key Addition layer the inverse MixColum layer is applied to the state. Note that just like in the final round of encryption, the first round of decryption does not use Inverse MixColumn.
In order to invert the MixColumn layer, we must use the inverse of the matrix used. Just like in encryption, the input is a 4-byte column of the state ‘C’, which is then multiplied by the inverse 4×4 matrix. The elements of the inverse matrix are still constants, and the operations (multiplication & addition) of the coefficients are still done in GF(28).
Here is a diagram of the mathematical description of the layer:
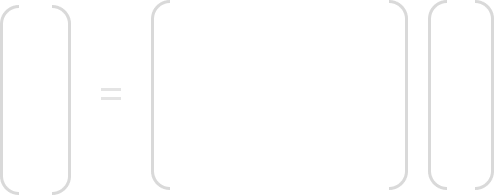
Here is an example of how we would compute B0 :
Example
B0 = 0E ⋅ C0 + 0B ⋅ C1 + 0D ⋅ C2 + 09 ⋅ C3
Note that these numbers 0E, 0B, 0D, and 09 are hexdecimal numbers, therefore these numbers have bit definitions for GF(28) polynomials. Therefore we must compute these in GF(28) meaning we need to follow addition and multiplication rules in GF(28). We went over that in Introduction to Galois Fields for AES. So if you are interested in learning that make sure to read that.
Inverse ShiftRows
To invert the ShiftRows layer operation from the encryption it is actually quite simple. We must simply shift the rows of the state matrix in the opposite direction. For instance, again the first row is not changed, and the rest of the rows instead of shifting right we shift left cylindrically.
In the Inv ShiftRow layer we shift each row cylindrically, meaning data rotates over. The rows are shifted by these rules:
- First row is not changed
- Second row is shifted 3 times to the left
- Third row is shifted 2 times to the left
- Fourth row is shifted 1 time to the left
Here is a diagram to better show how this works:

Inverse ByteSub
For the Inv ByteSub round we cannot reuse the S-Box used in encryption, we must use the inverse S-Box. But since the AES S-Box is a bijective, which means there is a one-to-one mapping, it is possible to construct the inverse S-Box in such a way that:
Ai = S-1 (Bi) = S-1 (S(Ai))
Where A and B are elements of the state matrix.
Just like in encryption for software implementations of AES, it is common that the inverse S-Box is a lookup-table, and is read in the same way as the non-inverse S-Box table. The inverse S-Box table can be seen below:
I mentioned this before, but if you remember how we read the S-Box, we read the inverse S-Box the same way but I will re-state that here. Recall that the input to the inverse S-Box is 1 byte= 8 bits. We use the first 4 bits for the row, and the last 4 bits for the column.
Check the example below to see how we do this:
Example
Let Bi = 7A16 (This is in hexadecimal)
We take the ‘716‘ to find the row and the ‘A16‘ for the column. So we get this:
S-1(Bi = 7A) = Ai = BD16 = 1011 11012.
The next section will cover how we mathematically comput this inverse S-Box table. This is not necessary to understand the functionality of AES. So the next section can be skipped if you wish. But I would suggest reading it if you want to implement AES in hardware as computing the values are usually faster than using the lookup table above.
Mathematical Description of the inverse S-Box
| Ai | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 52 | 09 | 6a | d5 | 30 | 36 | a5 | 38 | bf | 40 | a3 | 9e | 81 | f3 | d7 | fb |
| 1 | 7c | e3 | 39 | 82 | 9b | 2f | ff | 87 | 34 | 8e | 43 | 44 | c4 | de | e9 | cb |
| 2 | 54 | 7b | 94 | 32 | a6 | c2 | 23 | 3d | ee | 4c | 95 | 0b | 42 | fa | c3 | 4e |
| 3 | 08 | 2e | a1 | 66 | 28 | d9 | 24 | b2 | 76 | 5b | a2 | 49 | 6d | 8b | d1 | 25 |
| 4 | 72 | f8 | f6 | 64 | 86 | 68 | 98 | 16 | d4 | a4 | 5c | cc | 5d | 65 | b6 | 92 |
| 5 | 6c | 70 | 48 | 50 | fd | ed | b9 | da | 5e | 15 | 46 | 57 | a7 | 8d | 9d | 84 |
| 6 | 90 | d8 | ab | 00 | 8c | bc | d3 | 0a | f7 | e4 | 58 | 05 | b8 | b3 | 45 | 06 |
| 7 | d0 | 2c | 1e | 8f | ca | 3f | 0f | 02 | c1 | af | bd | 03 | 01 | 13 | 8a | 6b |
| 8 | 3a | 91 | 11 | 41 | 4f | 67 | dc | ea | 97 | f2 | cf | ce | f0 | b4 | e6 | 73 |
| 9 | 96 | ac | 74 | 22 | e7 | ad | 35 | 85 | e2 | f9 | 37 | e8 | 1c | 75 | df | 6e |
| A | 47 | f1 | 1a | 71 | 1d | 29 | c5 | 89 | 6f | b7 | 62 | 0e | aa | 18 | be | 1b |
| B | fc | 56 | 3e | 4b | c6 | d2 | 79 | 20 | 9a | db | c0 | fe | 78 | cd | 5a | f4 |
| C | 1f | dd | a8 | 33 | 88 | 07 | c7 | 31 | b1 | 12 | 10 | 59 | 27 | 80 | ec | 5f |
| D | 60 | 51 | 7f | a9 | 19 | b5 | 4a | 0d | 2d | e5 | 7a | 9f | 93 | c9 | 9c | ef |
| E | a0 | e0 | 3b | 4d | ae | 2a | f5 | b0 | c8 | eb | bb | 3c | 83 | 53 | 99 | 61 |
| F | 17 | 2b | 04 | 7e | ba | 77 | d6 | 26 | e1 | 69 | 14 | 63 | 55 | 21 | 0c | 7d |
This section will involve advanced algebra topics like Galoid Fields, if you are unfamiliar with the topic then I suggest first reading my post: Introduction to Galoid Fields for AES. With this post, you should be able to understand the following description below.
To compute the inverse S-Box we must do something similar to what we have been doing to the rest of the layers, and that is to reverse and/or invert the function. That is no different here. We first need to apply the inverse affine transformation on each Bi byte, then we need to apply the reversed Galois field inverse.
This can be viewed below:
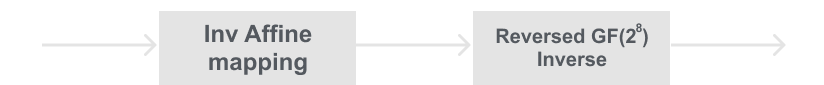
To reverse the S-Box substitution we first need to compute the inverse of the affine transformation. To do this, we take each input byte Bi (which is an element of GF(28)). Then apply the inverse affine transformation on each byte. Below is the inverse affine transformation on each byte Bi.

Note that (b7, …, b0) is the bitwise vector of the Bi(x) Byte, and (b’7 , …, b’0) is the result after the inverse affine transformation.
The second step to inverse the S-Box operation is to reverse the Galois Field inverse. Note that Ai = (Ai-1)-1. This means that all we need to do to reverse the Galoid Field Inverse is to compute the inverse again. This we have to compute:
Ai = (B’i)-1 ∈ GF(28)
Which again is reduced by our AES polynomial P(x) = x8 + x4 + x3 + x + 1. The zero-element is mapped to itself. Finally the result is the vector A = (a7, …, a0), and can be describe as:
Ai = S-1(Bi).
This has not been an intensive deep dive into the mathematical description of the inverse S-Box computation, but hopefully, this is a starting point for you to know where to start for your studies or implementations.
Decryption Key Schedule
Since the first round of decryption uses the last round key, the second round uses the second to last round key, and so on. We need the round keys in reversed order. Therefore a good way to achieve this is to compute the entire key schedule first, storing all the round keys, and then reversing the order of the key schedule. This would add a small time cost to the algorithm.
Code Implementation
Here is my code implementation of AES-128 in C++ this is done for educational purposes, and most ciphers are best suited for hardware. If you want to clone the repository or want to see more of my implementations you can check out my GitHub here.
main.cpp
/*
By: Hunter Richardson
Date: 9/5/2023
For the purpose of education
*/
#include <iostream>
#include <iomanip>
#include "helper.h"
#include "KeySchedule.h"
#include "Encryption.h"
#include "Decryption.h"
using namespace std;
int main()
{
Encryption encrypt;
Decryption decrypt;
KeySchedule key;
key.run();
encrypt.run();
decrypt.run();
printResult(encrypt.cipherText);
cout << endl;
printResult(decrypt.plainText);
}
KeySchedule.cpp
#include "KeySchedule.h"
void KeySchedule::run()
{
int round = 0;
while (round < 10)
{
if (round == 0)
{
for (int x = 0; x < 4; x++)
{
for (int y = 0; y < 4; y++)
{
roundKey[x][y][0] = key[x][y];
}
}
}
unsigned char temp[4] = { 0x00, 0x00, 0x00, 0x00 };
if (round == 0)
{
temp[0] = roundKey[0][3][0];
temp[1] = roundKey[1][3][0];
temp[2] = roundKey[2][3][0];
temp[3] = roundKey[3][3][0];
}
else
{
temp[0] = roundKey[0][3][round];
temp[1] = roundKey[1][3][round];
temp[2] = roundKey[2][3][round];
temp[3] = roundKey[3][3][round];
}
rotWord(temp, round);
subWord(temp, round);
rcon(temp, round);
round++;
for (int x = 0; x < 4; x++)
{
roundKey[x][0][round] = temp[x] ^ roundKey[x][0][round - 1];
}
for (int y = 1; y < 4; y++)
{
for (int x = 0; x < 4; x++)
{
roundKey[x][y][round] = roundKey[x][y][round - 1] ^ roundKey[x][y - 1][round];
}
}
}
}
void KeySchedule::rotWord(unsigned char temp[4], int round)
{
unsigned char temp2 = temp[0];
for (int x = 0; x < 4; x++)
{
temp[x] = temp[x + 1];
}
temp[3] = temp2;
}
void KeySchedule::subWord(unsigned char temp[4], int round)
{
for (int x = 0; x < 4; x++)
{
temp[x] = help.sBox[temp[x]];
}
}
void KeySchedule::rcon(unsigned char temp[4], int round)
{
temp[0] = temp[0] ^ RCon[round];
}
KeySchedule.h
#pragma once
#include "helper.h"
class KeySchedule
{
public:
unsigned char roundKey[4][4][11];
void run();
void rotWord(unsigned char temp[4], int round);
void subWord(unsigned char temp[4], int round);
void rcon(unsigned char temp[4], int round);
private:
Help help;
unsigned char key[4][4] = { {0x10, 0xd7, 0x74, 0xfb},
{0xa5, 0x4b, 0xcf, 0x47},
{0x88, 0xe5, 0x86, 0x38},
{0x69, 0xa3, 0x7c, 0x59} };
unsigned char RCon[10] = { 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36 };
};
Encryption.cpp
#include <iostream>
#include <iomanip>
#include "Encryption.h"
using namespace std;
void Encryption::run()
{
initializeCipherText();
key.run();
print3dArray(key.roundKey);
int round = 0;
print2dArray(cipherText);
for (int x = 0; x < 4; x++)
{
for (int y = 0; y < 4; y++)
{
cipherText[x][y] = cipherText[x][y] ^ key.roundKey[x][y][0];
}
}
round++;
while (round < 10)
{
subByte();
shiftRows();
mixColumns();
addRoundKey(round);
round++;
}
subByte();
shiftRows();
addRoundKey(round);
}
void Encryption::subByte()
{
for (int y = 0; y < 4; y++)
{
for (int x = 0; x < 4; x++)
{
cipherText[x][y] = help.sBox[cipherText[x][y]];
}
}
}
void Encryption::shiftRows()
{
int shift = 1;
for (int x = 1; x < 4; x++)
{
int index = 1;
while (index <= shift)
{
unsigned char first = cipherText[x][0];
for (int y = 0; y < 3; y++)
cipherText[x][y] = cipherText[x][y + 1];
index++;
cipherText[x][3] = first;
}
shift++;
}
}
void Encryption::mixColumns()
{
unsigned char temp[4] = { 0x00,0x00,0x00,0x00 };
unsigned char newState[4][4] = { {0,0,0,0},
{0,0,0,0},
{0,0,0,0},
{0,0,0,0} };
int rijndaelMatric[4][4] = { {2,3,1,1},
{1,2,3,1},
{1,1,2,3},
{3,1,1,2} };
for (int y = 0; y < 4; y++)
{
int z = 0;
for (int i = 0; i < 4; i++)
{
temp[i] = 0x00;
}
for (int x = 0; x < 4; x++)
{
for (int j = 0; j < 4; j++)
{
unsigned char constant = 0x00;
unsigned char element = 0x00;
switch (rijndaelMatric[z][j])
{
case 1:
temp[j] = cipherText[j][y];
break;
case 2:
element = cipherText[j][y];
temp[j] = multiplyBy2(element);
break;
case 3:
element = cipherText[j][y];
temp[j] = multiplyBy2(element) ^ element;
break;
}
}
newState[x][y] = int(temp[0]) ^ int(temp[1]) ^ int(temp[2]) ^ int(temp[3]);
z++;
}
}
for (int x = 0; x < 4; x++)
{
for (int y = 0; y < 4; y++)
{
cipherText[x][y] = newState[x][y];
}
}
}
void Encryption::addRoundKey(int round)
{
for (int x = 0; x < 4; x++)
{
for (int y = 0; y < 4; y++)
{
cipherText[x][y] = cipherText[x][y] ^ key.roundKey[x][y][round];
}
}
}
void Encryption::initializeCipherText()
{
switch (debug)
{
case 0:
break;
case 1:
for (int x = 0; x < 4; x++)
{
for (int y = 0; y < 4; y++)
{
cipherText[x][y] = 0x00;
}
}
break;
}
}
Encryption.h
#pragma once
#include "KeySchedule.h"
#include "helper.h"
class Encryption
{
public:
unsigned char cipherText[4][4];
void run();
private:
KeySchedule key;
Help help;
bool debug = 1; // BOOL DEBUG ACTIVE
void subByte();
void shiftRows();
void mixColumns();
void addRoundKey(int round);
void initializeCipherText();
};
Decryption.cpp
#include <iostream>
#include <iomanip>
#include "Decryption.h"
using namespace std;
void Decryption::run()
{
int round = 10;
initializePlainText();
key.run();
invAddRoundKey(round);
invShiftRows();
invSubByte();
round--;
while (round > 0)
{
invAddRoundKey(round);
invMixColumns();
invShiftRows();
invSubByte();
round--;
}
invAddRoundKey(round);
}
void Decryption::invSubByte()
{
for (int y = 0; y < 4; y++)
{
for (int x = 0; x < 4; x++)
{
plainText[x][y] = help.InvsBox[plainText[x][y]];
}
}
}
void Decryption::invShiftRows()
{
int shift = 1;
for (int x = 1; x < 4; x++)
{
int index = 1;
while (index <= shift)
{
unsigned char last = plainText[x][3];
for (int y = 3; y > 0; y--)
plainText[x][y] = plainText[x][y - 1];
index++;
plainText[x][0] = last;
}
shift++;
}
}
void Decryption::invMixColumns()
{
unsigned char temp[4] = { 0x00,0x00,0x00,0x00 };
unsigned char newState[4][4] = { {0,0,0,0},
{0,0,0,0},
{0,0,0,0},
{0,0,0,0} };
int rijndaelMatric[4][4] = { {14,11,13,9},
{9,14,11,13},
{13,9,14,11},
{11,13,9,14} };
for (int y = 0; y < 4; y++)
{
int z = 0;
for (int i = 0; i < 4; i++)
{
temp[i] = 0x00;
}
for (int x = 0; x < 4; x++)
{
for (int j = 0; j < 4; j++)
{
unsigned char constant = 0x00;
unsigned char element = 0x00;
switch (rijndaelMatric[z][j])
{
case 9:
element = plainText[j][y];
temp[j] = (multiplyBy2(multiplyBy2(multiplyBy2(element)))) ^ element;
break;
case 11:
element = plainText[j][y];
temp[j] = (multiplyBy2(multiplyBy2(multiplyBy2(element)) ^ element)) ^ element;
break;
case 13:
element = plainText[j][y];
temp[j] = multiplyBy2(multiplyBy2(multiplyBy2(element) ^ element)) ^ element;
break;
case 14:
element = plainText[j][y];
temp[j] = multiplyBy2((multiplyBy2(multiplyBy2(element) ^ element)) ^ element);
break;
}
}
newState[x][y] = int(temp[0]) ^ int(temp[1]) ^ int(temp[2]) ^ int(temp[3]);
z++;
}
}
for (int x = 0; x < 4; x++)
{
for (int y = 0; y < 4; y++)
{
plainText[x][y] = newState[x][y];
}
}
}
void Decryption::invAddRoundKey(int round)
{
for (int x = 0; x < 4; x++)
{
for (int y = 0; y < 4; y++)
{
plainText[x][y] = plainText[x][y] ^ key.roundKey[x][y][round];
}
}
}
void Decryption::initializePlainText()
{
switch (debug)
{
case 0:
break;
case 1:
for (int y = 0; y < 4; y++)
{
for (int x = 0; x < 4; x++)
{
plainText[x][y] = nist[y][x];
}
}
break;
}
}
Decryption.h
#pragma once
#include "KeySchedule.h"
#include "helper.h"
class Decryption
{
public:
unsigned char plainText[4][4];
void run();
private:
KeySchedule key;
Help help;
bool debug = 1; // BOOL DEBUG ACTIVE
unsigned char nist[4][4] = { {0x6d, 0x25, 0x1e, 0x69},
{0x44, 0xb0, 0x51, 0xe0},
{0x4e, 0xaa, 0x6f, 0xb4},
{0xdb, 0xf7, 0x84, 0x65} };
void invSubByte();
void invShiftRows();
void invMixColumns();
void invAddRoundKey(int round);
void initializePlainText();
};
helper.cpp
#include <iostream>
#include <iomanip>
#include "helper.h"
using namespace std;
void printResult(unsigned char array[4][4])
{
for (int x = 0; x < 4; x++)
{
for (int y = 0; y < 4; y++)
{
cout << hex << setfill('0') << setw(2) << int(array[y][x]);
}
}
}
unsigned char multiplyBy2(unsigned char element)
{
unsigned char constant = ((element & 0x80) == 0x80) ? 0x1b : 0x00;
return (element << 1) ^ constant;
}
helper.h
#pragma once
class Help
{
public:
unsigned char sBox[256] = {
0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16
};
unsigned char InvsBox[256] = {
0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D,
};
};
void printResult(unsigned char array[4][4]);
unsigned char multiplyBy2(unsigned char element);
Security of AES
The Advanced Encryption Standard (AES) is still one of the most used ciphers in the world due to its security. In fact, it is believed that AES-256 is quantum-resistant, meaning it is not believed that quantum computers will be able to break AES-256 faster than a classical computer (Recall that AES-256 refers to the AES cipher with a 256-bit key).
To put the security of AES into perspective just using AES-128, which is AES with a 128-bit key. Using my machine and my implementation I can generate ~16 million keys a second (using my cpu), and I need to test all 2128 keys, that is 340 undecillion 282 decillion 366 nonillion 920 octillion 938 septillion 463 sextillion 463 quintillion 374 quadrillion 607 trillion 431 billion 768 million 211 thousand 456 keys. Lets say I have a long lost grandparent who gave me their fortune and I bought 1 billion replicas of my machine, then I can generate ~16 Quadrillion keys per second, that is 16,000,000,000,000,000 keys per second. There are ~31,536,000 seconds in a year, thus in a year my billion machines could generate ~504 Sextillion keys per year. If I then ran all billion machines at once, checking all keys until I tried them all it would still take ~674 Trillion years to find the key.
To put that into perspective, the universe has existed for ~14 Billion years. It would take ~48,164 Thousand times longer than the age of the universe to exhaust the entire key space of just AES-128. That is not to mention AES-192 which is 64 times larger, or AES-256 which is 128 times larger than AES-128.













