Modes of Operation for Block Ciphers

Introduction

Today we won’t actually learn about any new math concepts or algorithms. Instead, we will build upon what we have already. Particularly how we encrypt a plaintext that is larger than a block cipher’s block size (e.g. AES 16 bytes and DES 8 bytes). In practice, we typically want to encrypt more than one single 8-byte or 16-byte plaintext like when encrypting an email or file.

Our current way of viewing how we would do this with a block cipher is like below:

We simply encrypt one block after another, and concatenate the cipher text that is then sent to your recipient. But interestingly this is not the only way to do this, in fact, this is a pretty bad way to do it. The different methods of how we do this we called Modes of Operation. Here are several popular modes of operation:

Galois/Counter Mode (GCM)
Electronic Codebook (ECB)
Cipher Block Chaining (CBC)
Cipher Feedback (CBC)
Output Feedback (OFB)
Counter (CTR)

In this post, we will only focus on ECB, CBC, and OFB. I believe these are good building blocks for you to learn more about the other Modes of Operations on your own if you wish to in the future.

Electronic Codebook Mode (ECB)

Imagine you have a pdf file and you are trying to use AES to encrypt it. The question is then how do we encrypt the entire file securely? The straightforward way to go is ECB, and in fact, ECB is the same as the example given in the Introduction. In the Electronic Codebook mode, you take your block cipher, feed in all your plaintext blocks, encrypt all the data one at a time, and concatenate the ciphertext blocks together. Below is a diagram of this:

Definition: Electronic Codebook Mode (ECB)

Let e() be a block cipher of block size n, and let x_i and y_i be bit strings of length n.

Encryption: y_i = e_k(x_i), i ≥ 1
Decryption: x_i = e_k^-1(y_i) = e_k^-1(e_k(x_i)), i ≥ 1

There are advantages to using ECB. For instance, if the receiver does not for some reason receive all the encrypted blocks they could still decrypt what they received. If there was a bit error or a flip it would only affect the block that the error occurred in. Also, block ciphers using ECB mode could paralyze encryption making encryption and decryption faster.

However, as is often the case in cryptography, there are unexpected weaknesses with the ECB mode. To show you this weakness I’ll show you an attack that exploits ECB’s weakness.

Substitution Attack Against ECB

Imagine a scenario between two banks. The two banks are part of a large network like the Internet (In practice most banks would use a proprietary connection), and the banks use this channel to transfer data:

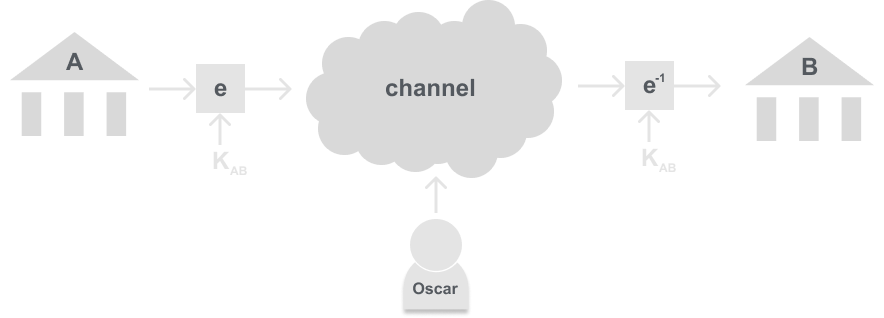
Now imagine both Bank A and B decided to use ECB with their block cipher. They also decided on a simple transfer protocol, so that if a bank wants to transfer money they send the request formatted as:

We have to now make a few assumptions:

Each block (1, …, 5) is exactly n bits long.
The key K_AB is fixed for some time. Meaning it does not change frequently.
Oscar is an active attacker. Meaning he can not only see the traffic on the channel but can also manipulate the traffic.

Now to complete this attack Oscar needs to:

Oscar opens one account at Bank A, and one account at Bank B.
Oscar taps the encrypted channel between the banks.
Oscar transfers $1.00 repeatedly from his account at Bank A to his account at Bank B. He then observes the ciphertexts going through the channel. He then checks for ciphertext blocks that repeat. Note that he can do this even though the data is still encrypted with AES because the ciphertext is the same each time. Oscar then stores blocks 1, 3, and 4 from these transfers. Recall these are encrypted versions of Bank A’s Identifier, Bank B’s Identifier, and his own encrypted version of his receiving account #.
Recall that the two banks do not change the key often. This means that the same key is used for several transfers between Bank A and Bank B. Therefore Oscar can compare blocks 1 and 3 of all subsequent messages with the ones he has stored. To clarify Oscar is now identifying each transaction where Bank A is sending money to an account at Bank B. Oscar now just simply replaces block 4 (which is the Bank B receiving account number) with the encrypted block 4 that he stored before. Resulting in all transfers from some account at Bank A being redirected to the Oscars Bank B account.
Quickly withdraw all the money from Bank B and fly to a country with no policy on extradition for white-collar crimes!

What is interesting about this very illegal get-rich-quick scheme is that it works without attacking the block cipher itself. So even if the banks used a cipher like AES-256, they still could not prevent the attack using the ECB Mode of Operation. This sort of attack is called a violation of the integrity of the message. To note there are available techniques for preserving the integrity of a message, namely message authentication codes (MACs) and digital signatures. Both are widely used to prevent such an attack. These techniques are a topic for another time though.

You may notice that this attack is actually similar to the letter frequency analysis attack covered in The Substitution Cipher post. There we noticed the one-to-one mapping of letters in the alphabet. Here is is still a one-to-one mapping of 128 plaintext bits to 128 ciphertext bits. In this case, instead of having an alphabet of 26 letters, we have an alphabet of 2¹²⁸. This is why it is called the Electronic Codebook because theoretically, we could make a lookup book with all 2¹²⁸ possible inputs and outputs with a given key.

Conclusion

The Electronic Codebook mode is an expected way to solve out problem of encrypting multiple plaintext blocks, but in practice is very insecure. So we want a mode that if we give the same plaintext and key we get a different ciphertext out every time.

Cipher Block Chaining Mode (CBC)

There are two problems we want to improve upon based on what we observed in the ECB mode. Those two problems we are gonna fix in the Cipher Block Chaining Mode (CBC) are:

Make encryption probabilistic.
Combine encryption of all blocks.

You may be wondering what I mean by probabilistic, here is the definition:

Definition: Deterministic

An encryption scheme is deterministic if a particular plaintext is mapped to a fixed ciphertext if the key is unchanged.

Therefore we will say that an encryption scheme is probabilistic if it uses randomness to achieve non-deterministic generation of the ciphertext. Here is a diagram to further show the difference between a deterministic and probabilistic scheme:

Deterministic

Probabilistic

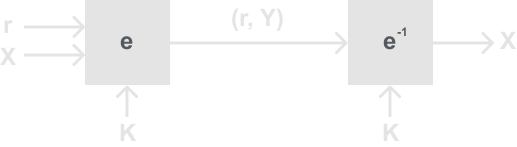
The first thing you may notice is that the electronic codebook mode (ECB) is a deterministic scheme. The change we made in the probabilistic scheme is that instead of just sending the plaintext you also introduce a random value r which is also sent along with the ciphertext. Therefore r doesn’t have to be a secret, that is because for the receiver to decrypt, they must need the random value as well. In the case of CBC, this random value we will use is called the Initial Vector, or IV for short. It is also important to state that the IV should be a nonce (number used only once), if it is not then we could have the same problem of getting repeat ciphertext blocks from the same plaintext block. If the IV was not a nonce then we could use the same attack outlined in the ECB mode above.

You may wonder how this could help at all if we are just gonna allow and person listening to the channel to know the random value anyway. To answer that concern let me first introduce the cipher block chaining mode (CBC) with a diagram below:

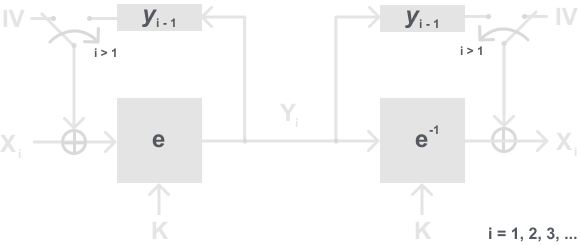
It may be a little hard to understand in just a diagram but how CBC mode works is it uses an IV (Initial Vector) which is the XORd with the first block before being encrypted by the block cipher. Then after the first, all subsequent blocks are instead XORd with the previously encrypted block. For example, when encrypting the first block x₁ it is first XORd with the IV, encrypted with the block cipher giving y₁. Then the block x₂ instead of being XORd with the IV is now XORd with the new ciphertext y₁ (recall that y₁ was dependent on x₁), then encrypted, giving y₂. This goes on until all plaintext blocks are encrypted this way. Resulting in chaining together of all the plaintext blocks because each block is now dependent on all the subsequent blocks.

For decryption using CBC mode, it is slightly different because we must do the inverse of encryption. In the CBC case, we only used XOR, and as you may recall XOR is the inverse of itself. Therefore all we must do is take our y_i ciphertext blocks, use our block cipher decryption algorithm, and then XOR with the correct value before getting the plaintext back out. For example, we first take our first ciphertext block y₁, decrypt, then XOR with the IV (which recall is known/ sent over the channel), giving plaintext x₁ back out. Then we take y₂, decrypt, and then use the y₁ block that we saved and XOR, giving x₂. Again this repeats till we have decrypted the entire message.

Definition: Cipher Block Chaining Mode (CBC)

Let e() be a block cipher of block size n, let x_i and y_i be bit strings of length n, and IV be a nonce of length n.

Encryption (first block): y₁ = e_k(x₁ ⊕ IV)
Encryption (remaing blocks): y_i = e_k(x_i ⊕ y_i-1), i≥ 2
Decryption (first block): x₁ = e_k^-1(y₁) ⊕ IV
Decryption (remaining blocks): x_i = e_k^-1(y_i) ⊕ y_i-1, i≥ 2

We now need to know how we derive the IV. Recall that the IV should be a nonce, so we need to choose a new IV every time we encrypt so that the CBC mode becomes a probabilistic encryption scheme. This means that if we encrypt a string of plaintext blocks once with an IV, and we encrypt the same blocks again with another IV, the two ciphertexts look completely different to an attacker.

Thus how can we generate these IVs?

Use a True Random Number Generator (TRNG), and send the plaintext IV along with the ciphertext. This has a drawback that you need to ensure you don’t reuse values. So each time you generate an IV you need to store it and check that you haven’t used it before.
A counter. Both parties start on the same value, and each time a new ciphertext is sent you iterate the counter once. This is a very simple and effective way to generate IVs because there is no fear of reusing IVs and you don’t even need to send it on the channel because both parties have it.
Concatenate a pseudo-random value with some identifiers, e.g. ID_A || ID_B || (time in milliseconds message was sent). This method highly reduces the chance someone else on the channel is using the same IV.
etc

The Cipher Block Chaining mode is a very popular and effective mode to use and will suit many cases. But there is still a slight problem with it, which is that it still requires padding at the end of a message to fill out a block if the data doesn’t perfectly fit. This could introduce some insecurities if padded incorrectly. The next mode will solve this problem.

Output Feedback Mode (OFB)

The Output Feedback mode (OFB) uses the block cipher to build a stream cipher encryption scheme. If you recall Stream Ciphers, Random Numbers, and the One-Time-Pad, one big problem was designing a cryptographically secure pseudo-random number generator (PRNG). Thus the idea behind OFB mode is to use a proven cryptographically secure block cipher like AES and use that as a key stream generator (KSG).

One way we made the KSG was in Stream Ciphers cont’d and Linear Feedback Shift Registers where we used a LFSR to generate the key stream bits. In OFB we will use the block cipher as the key stream generator as below:

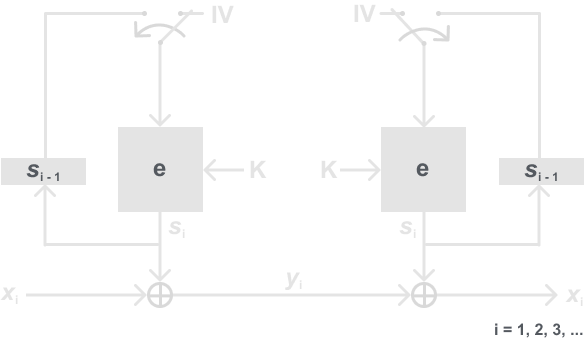
You may first notice that we are not using e-1 when generating the key stream bits for decryption. We instead are using the block cipher encryption algorithm on both sides. Why is that? That is because we are not actually using the block cipher for encryption, therefore we do not need to inverse the block cipher. We are using the XOR operation in encrypt, and the inverse of XOR is itself again. We are using the encryption algorithm as a PRNG, thus we need to derive the same key stream on both ends. Resulting in using the same method to generate the key stream bits on both ends.

In some ways, the OFB mode is similar to the CBC mode. But at no point are we actually using the block cipher to encrypt the actual plaintext, we are simply using the output bits as a key stream to XOR so that we can make a stream cipher. To really make sure this point sticks, a stream cipher is as secure as the key stream generator is. So by using a block cipher like AES, we can make a cryptographically strong pseudo-random key stream generator like we need.

Definition: Output Feedback Mode (OFB)

Let e() be a block cipher of block size n, let x_i, y_i and s_i be bit strings of length n, and IV be a nonce of length n.

Encryption (first block): s₁ = e_k(IV) and y₁ = s₁ ⊕ x₁
Encryption (remaing blocks): s_i = e_k(s_i-1) and y_i = s_i ⊕ x_i , i ≥ 2
Decryption (first block): s₁ = e_k(IV) and x₁ = s₁ ⊕ y₁
Decryption (remaining blocks): s_i = e_k(s_i-1) and x_i = s_i ⊕ y_i, i ≥ 2

As a result of using a nonce IV, the OFB mode is probabilistic. Meaning if we encrypt the same plaintext twice we result in different ciphertexts.

Another result of using OFB is that it solves the small problem we saw in CBC. Which was that in the CBC mode, we still needed to pad the plaintext if the plaintext didn’t perfectly fit into all the blocks. That is because we are not encrypting by block in OFB, it is a stream cipher, so we can encrypt bit by bit. This is also still a fast mode because in practice it is not necessary to encrypt bit by bit. Since we are generating key stream bits n bits at a time, we can XOR n plaintext bits at a time by paralyzing the software/ hardware.

Conclusion

It is always important to not only look at the methods we use but also at how we implement them. It doesn’t matter how secure an algorithm we make if we are implementing it in an insecure way.

If you are still interested in more modes of operations for block ciphers I suggest you look into the following modes: