Introduction
This is the beginning of asymmetric cryptography for this series of posts, so if you are just now beginning to follow along with these posts (firstly, thank you) I have good news. Very little from the posts before are needed to understand asymmetric cryptography. But that doesn’t mean we won’t ignore all of it, there are still some posts I recommend you are familiar with first so that you can follow along. Here are the posts I recommend, I will also link posts I am referencing as needed so don’t feel like you need to read them all now:
Today we are not actually doing any cryptography (which may be weird for a cryptography blog, but the basics are important). This post will be all about the mathematics used in asymmetric cryptography. That is because, unlike symmetric cryptography, asymmetric cryptography heavily relies on the mathematics that the ciphers are based on for security
If it makes you feel any better, the maths we will discuss below you may have seen already. But if you haven’t I will be sure to give examples and give detailed descriptions. But before we delve into that let’s recall the principles of symmetric cryptography, and compare them to the principles of asymmetric cryptography.
Principles of Symmetric Cryptography
Recall from the post What is Cryptology the basic symmetric encryption scheme:
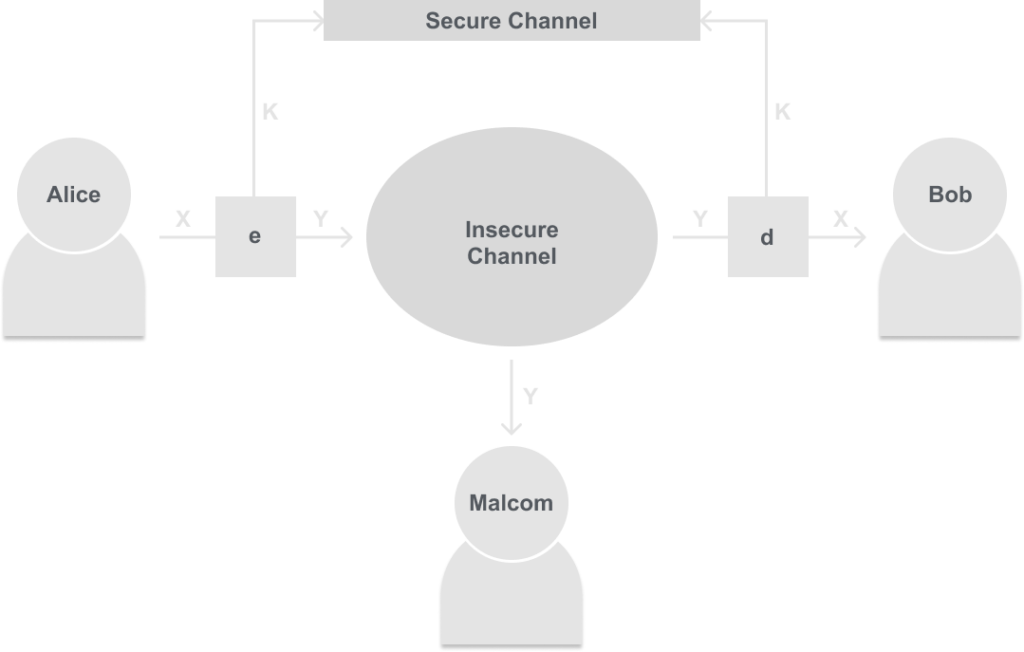
In symmetric cryptography, the two properties are true:
- The same secret key is used for encryption and decryption.
- The encryption and decryption algorithms are very similar.
Modern symmetric algorithms like AES, which we talked about in (AES) The Advanced Encryption Standard are very secure, and fast and are used in most machines. However, there are still some problems that occur when we focus our scope on more than just encrypting data. Namely, these are some of those problems.
Key Distribution: Notice in the model above the basic symmetric encryption scheme before Alice and Bob can communicate securely they first must establish a secure channel.
Number of Keys: Imagine you are a large company or just an individual with friends who want to only communicate securely with symmetric cryptography. You would run into the problem of needing a different key for each person you want to talk with. This can become problematic very easily.
Authentication: Imagine you are Alice, and instead of communicating with another person like Bob you are communicating with Amazon.com. Since you are using symmetric cryptography, you both need the same key. But now we run into the issue if someone is dishonest, or a third party retrieves the key. Since a message could originate from either Alice or Amazon, who is to say Malcolm doesn’t place an order using the key that Amazon fulfills? But since Amazon thinks the order came from Alice since Alice is the only person that is supposed to have the other key they charge Alice for Malcom’s order. So now how is Amazon supposed to authenticate the message didn’t come from Alice, and she is just trying to cheat the system.
Principles of Asymmetric Cryptography
In order to overcome the drawbacks of symmetric cryptography. A few people had a great idea to come up with asymmetric cryptography. They had the idea that it is not essential that the key possessed by the person who encrypts the message (Alice in our scenario) is secret. The crucial part is that the recipient (Bob) can only decrypt using a secret key. In order to do this Bob publishes a public encryption key for everyone to know. But Bob keeps his private decryption key, which he only knows. Thus Bob’s key consists of two parts, a public part kpub, and a private one, kpr.
An analogy to this is to imagine a ballot box. Everyone can put their vote in the box, but only the person with the secret key to open the box can see the votes.
The basic scheme for asymmetric cryptography looks like:
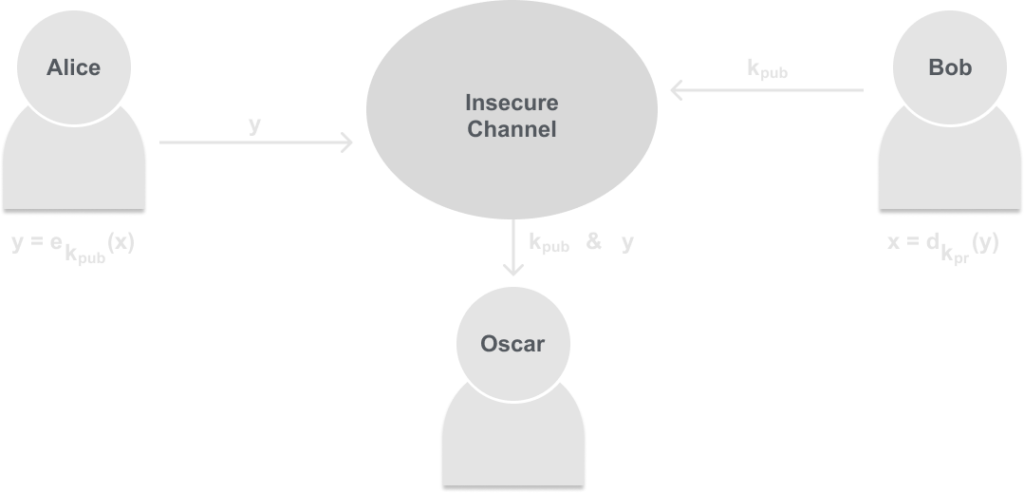
Notice that even though the attacker in this case we will call him Oscar can see the kpub sent by Bob and the ciphertext y sent by Alice. But Oscar is not able to decrypt Alice’s message with kpub, to decrypt, Oscar would need kpr, which only Bob has.
This is the basis of asymmetric cryptography, also called public-key cryptography.
Uses of Public-Key Cryptography
As shown in the last section, public key schemes can be used for encrypting data. But it turns out that this is not the best use of public-key cryptography, and in fact, can do what was previously unimaginable with symmetric cryptography. The main things we can do with public-key cryptography, and which will be discussed in greater detail in future posts are:
- Key Establishment
- Nonrepudiation
- Identification
- Authentication (MACs)
- Encryption
- etc
Mathematics Essential for Asymmetric Cryptography
As mentioned above, the bulk of this post will be setting a good foundation for the maths needed for public-key cryptography. So I will show some techniques from number theory that are essential for asymmetric cryptography.
Euclidean Algorithm
If you are not familiar with the Euclidean algorithm or need a reminder, the Euclidean algorithm is used for finding the greatest common divisor or GCD of two numbers.
Lets start with the problem of first finding the greatest common divisor of two numbers.
Example: Given two numbers r0 = 27, r1 = 21, find the gcd(r0, r1) = ?
Factoring these two numbers gives:
r0 = 27 = 3 * 3 * 3.
r1 = 21 = 3 * 7.
Thus the greatest common divisor is gcd(27, 21) = 3.
This is probably the way most were taught, and still the first way we think to go about finding the gcd of two numbers. But this will not work for all numbers (won’t be fast/ practical), particularly with big numbers, and in asymmetric cryptography, we want to use those big numbers.
So are there any methods that would work? Yes, and surprise surprise the Euclidean algorithm will work! The Euclidean algorithm is based on the simple observation that:
gcd(r0, r1) = gcd(r0 mod r1, r1) = gcd(r1, r0 mod r1)
Notice how this could help our problem in asymmetric cryptography which requires large numbers, but needs a fast algorithm. Using this idea we can reduce the size of our original numbers using modular arithmetic. If you are unfamiliar with modular arithmetic make sure to take a minute to read my Introduction to Modular Arithmetic post.
Lets see an example of how this works:
Example: Given two numbers r0 = 27, r1 = 21, find the gcd(r0, r1) = ?
Using the observation stated above:
gcd(27, 21) = gcd(27 mod 21, 21).
= gcd(6, 21).
= 3.
Notice that we have already reduced the problem to an easier case. But what if it still wasn’t easy enough for us to do in our head? Well, we could just do it again!
gcd(6, 21) = gcd(21 mod 6, 6).
= gcd(3, 6).
= gcd(6 mod 3, 3).
= gcd(0, 3).
= 3.
Thus the greatest common divisor is gcd(27, 21) = 3.
But if you recall from Introduction to Modular Arithmetic, we had another way to write a modular operation. Lets see what we get when we try that way:
Example: Given two numbers r0 = 27, r1 = 21, find 27 mod 21 = ?
Using the other method in a past post:
27 = 21 ⋅ 1 + 6
21 = 6 ⋅ 3 + 3
6 = 3 ⋅ 2 + 0
Recall that in this method we would use the remainder as the next value multiplied by some quotient for the next reduction. Then we would continue until the remainder were 0, and the answer would be the remainder before 0. So in this case 3. Also notice this is gcd(27, 21) = 3, and this is the case for all numbers.
It is also helpful to look at this algorithm with slightly larger numbers. If you are interested I highly suggest you try to solve this problem on your own first using the method above, then checking your answer. But the answer is there any way if you don’t feel like doing it yourself first.
Try to solve gcd(973, 301) using the method above:
Example: Given two numbers r0 = 973, r1 = 301, find gcd(973, 301) = ?
Using the other method in a past post:
973 = 301 ⋅ 3 + 70.
301 = 70 ⋅ 4 + 21.
70 = 21 ⋅ 3 + 7.
21 = 7 ⋅ 3 + 0.
Therefore the gcd(973, 301) = 7. If you wish you can also use the first simple observation noted first to get the same answer!
Now that we have the basics, let’s try to abstract this problem with a more formal description of the Euclidean algorithm in the form of pseudo-code below:
Pseudo Code: Euclidean Algorithm
Let r0 and r1 be integers withr0 > r1. The output will be gcd(r0, r1). To initialize the algorithm let i = 1.
DO
i = i + 1
ri = ri – 2 mod ri – 1
WHILE ri != 0
RETURN
gcd(r0, r1) = ri – 1
Note that the algorithm actually terminates once it computes a remainder of 0. Then the remainder previously computed is the answer to our gcd problem.
Not too bad huh? We now have a faster way for computers to compute the greatest common divisor between two numbers no matter how large without factoring. But we still need a bit more out of the algorithm to properly implement public-key cryptography. That will be where the extended Euclidean algorithm comes in.
Extended Euclidean Algorithm
We have seen how we can use the Euclidean algorithm to find the greatest common divisor of two numbers. However, as it turns out the main use of the Euclidean algorithm in public-key cryptography is not just finding the gcd. In the extension of the Euclidean algorithm, which we call the extended Euclidean algorithm we can compute modular inverses. This will not be obvious at first, but keep that in the back of your mind as you read this section that we are doing this to compute modular inverses.
The idea of the extended Euclidean algorithm is given two numbers r0 and r1. We compute a linear combination:
gcd(r0, r1) = s ⋅ r0 + t ⋅ r1.
Where s and t are coefficients. Notice that in the extended Euclidean algorithm, we are not only computing the gcd but also getting these new coefficients s and t. But now we need to know how we do this.
Well, the left half (gcd(r0, r1)) is easy, we just did it in the last section. We just use the Euclidean algorithm. But now in addition we have to compute s and t, and sadly these are kind of a pain in the neck. The idea behind doing this is to use our original equation representation of modular reduction we used in the observation example in the last section. Now that we have the remainder ri from each iteration, we express ri as a linear combination of the form:
ri = si ⋅ r0 + ti ⋅ r1.
Then just as in the Euclidean algorithm, once we compute a remainder rl = 0 (where ‘l’ is the index for the last iteration) we terminate the algorithm and we use the s and t from the previous remainder as our s and t coefficients.
You may have realized that I just typed a lot of words without really answering the question of how we actually compute s and t. To show that let’s go back to that fourth example in the last section. This is why I thought it would be a good idea to do that example yourself first to better understand this part:
Example: Given two numbers r0 = 973, r1 = 301, find gcd(973, 301) = 7 (as found before).
i
2 973 = 301 ⋅ 3 + 70, r2 = 70 = 1 ⋅ 973 + (-3) ⋅ 301.
3 301 = 70 ⋅ 4 + 21, r3 = 21 = 301 – 4 ⋅ 70.
= 301 ⋅ 1 – 4(973 ⋅ 1 + (-3) ⋅ 301).
= (-4) ⋅ 973 + (13) ⋅ 301.
4 70 = 21 ⋅ 3 + 7, r4 = 7 = 70 – 21⋅ 3.
= (1 ⋅ 973 + (-3) ⋅ 301) – 3((-4) ⋅ 973 + (13) ⋅ 301).
= (13) ⋅ 973 + (-42) ⋅ 301.
21 = 3 ⋅ 7 + 0
(*Notice that we just reordered the original equations to solve for the remainder)
Therefore, gcd(973, 301) = 7 = (13) ⋅ 973 + (-42) ⋅ 301. This means we have gotten our coefficients s = 13 and t = -42.
It is important to note the algebra used in the example above. I tried my best using highlights, but really took a minute to understand how each equation is constructed using the results of the previous linear combinations. This is important because if we can observe that, then we can make a recursive formula to compute si and ti in each iteration as seen below:
Recursive Formulae: Extended Euclidean Algorithm
Assume we are on the iteration of i. Then in the last two iterations, we computed:
ri – 2 = (si – 2) ⋅ r0 + (ti – 2) r1.
ri – 1 = (si – 1) ⋅ r0 + (ti – 1) r1.
Recall that we also compute the quotient qi – 1 as well using the Euclidean algorithm:
ri – 2 = (qi – 1) ⋅ (ri – 1)+ ri.
*rewriting to solve for ri.
ri = ri – 2 – (qi – 1) ⋅ (ri – 1).
Now we can substitute ri – 2 and ri – 1:
ri = ((si – 2) ⋅ r0 + (ti – 2) r1) – (qi – 1) ⋅ ((si – 1) ⋅ r0 + (ti – 1) r1).
= [si – 2 – qi – 1 ⋅ si – 1] ⋅ r0 + [ti – 2 – qi – 1 ⋅ ti – 1] ⋅ r1.
Then we can just let these be our si and ti:
ri = [si] ⋅ r0 + [ti] ⋅ r1.
We also get recursive formulae to compute si and ti:
si = si – 2 – (qi – 1) ⋅ (si – 1).
ti = ti – 2 – (qi – 1) ⋅ (ti – 1).
This is true for i > 1. The initial values we need to start this recursive formula are:
s0 = 1, s1 = 0.
t0 = 0, t1 = 1.
i = 1.
Why these initial values? To be honest the reasoning is sorta of out of the scope of this already long and math-heavy post. I suggest you do your own research if you are interested in this topic, but for most, this would be overkill.
Now that we understand how to get these s and t coefficients, let’s go back and try to answer why we wanted these coefficients in the first place. I alluded to it at the beginning, but the short answer is modular inverses.
Let’s take a step back and look at the problem we wanted to solve, which is given a number a, what is its modular n inverse (i.e. a-1 ≡ ? mod n). Recall from The Shift Cipher, particularly when we talked about the affine cipher that by definition an inverse satisfies a-1 ⋅ a ≡ 1 mod n. So how can we use the extended Euclidean algorithm to give us a-1?
Recall that from the extended Euclidean algorithm we compute:
gcd (n, a) = 1 = s ⋅ n + t ⋅ a = 1.
Not take this equation and reduce by modulo n:
s ⋅ n + t ⋅ a mod n= 1 mod n.
= t ⋅ a = 1 mod n.
If you do not see it yet, compare that result with the observation we made that an inverse must satisfy a-1 ⋅ a ≡ 1 mod n. Then we can conclude that t = a-1! We have just computed the modular inverse of a value a, which is a lot faster and easier than our previous method of brute forcing it with the affine cipher.
*note gcd(n, a) = 1 was discussed in The Shift Cipher and is necessary for an element to have an inverse.
The good news is the end of the hard stuff. The rest of the post will be about important theorems that will be important for future posts when we talk about algorithms in asymmetric cryptography. The theorems will only be presented, I won’t bore you with the proofs of these theorems. But if you like that kinda stuff I highly encourage you to take the time and read them yourself!
Euler's Phi Function
The Euler’s Phi Function is a very useful theorem in public-key cryptography, and especially in the next algorithm we will discuss RSA. You may have heard before on the news, or surrounding the discussion around post-quantum cryptography that the security behind RSA is how hard it is to factor two large prime numbers. In essence that is because Euler’s Phi Function is the backbone of RSA, and Euler’s Phi Function uses those prime factorizations.
For the Euler’s Phi Function consider a ring ∈ ℤm = { 0, 1, 2, …, m – 1}, if you need a refresher on what a ring is I recommend you read Introduction to Modular Arithmetic. We are interested in finding how many elements in ℤm are relatively prime to m, i.e. if gcd(a, m) = 1. The total amount of these relatively prime elements are given by the Euler’s Phi Function, defined as:
Definition: Euler’s Phi Function.
The number of integers in ℤm relatively prime to m is denoted by ϕ(m).
Let’s see an example, and calculate Euler’s Phi Function by brute force checking all integers in ℤm which are relatively prime to m. Thankfully we already know how to get the greatest common divisor of two numbers using Euclidean’s algorithm.
Example: Let m = 6. Then ℤ6 = {0, 1, 2, 3, 4, 5}. What is ϕ(6) = ?.
gcd(0, 6) = 6.
gcd(1, 6) = 1.
gcd(2, 6) = 2.
gcd(3, 6) = 3.
gcd(4, 6) = 2.
gcd(5, 6) = 1.
Since there are 2 integers in ℤ6 that are relatively prime to 6 (1 and 5), the result we get is ϕ(6) = 2.
As you can imagine, and as was a problem in the above sections simple solutions like these sometimes don’t work for large numbers. These are exactly the type of numbers we require in public-key cryptography, and in fact, finding Euler’s Phi Function this way is out of reach. You can try to do it, but if you are working with numbers required for RSA the list you make would be longer than atoms in the universe. So we need another way. Fortunately, there is a way to find Euler’s Phi Function a lot faster as long as we know the factorization of m.
Theorem: Let m have the following canonical factorization:
m = p1e1 ⋅ p2e2 ⋅… pnen .
where the pi are distinct prime numbers and ei are positive integers, then:
ϕ(m) = ∏i = 1n (piei – piei – 1).
This is faster because typically the value n (the number of distinct prime factors) is small even for large numbers, evaluating the product (∏) is very easy. Let me show you an example to better show this.
Example: Let m = 240. Then ℤ240 = {0, 1, 2, …, 239}. What is ϕ(240) = ?.
m = 16 ⋅ 15 = 24 ⋅ 31 ⋅ 51 = p1e1 ⋅ p2e2 ⋅ p3e3 .
then we can write the Euler’s Phi Function as:
ϕ(240) = ∏i = 13 (piei – piei – 1) = (24 – 23) ⋅ (31 – 30) ⋅ (51 – 50) = 8 ⋅ 2 ⋅ 4 = 64.
This means there are 64 integers in ℤ240 that are coprime to m = 240.
I want to stress, especially because we will discuss RSA in the next post that we need to know the factorization of m in order to calculate Euler’s Phi Function quickly to use this theorem. Therefore, how difficult to find the factorization is at the heart of RSA public-key scheme. Conversely, if we know the factorization we can compute Euler’s Phi Function and decrypt the ciphertext.
The last two theorems are important but not as integral as Euler’s Phi Function. So I will only mention them briefely.
Fermat's Little Theorem
Fermat’s little theorem is primarily used in public-key cryptography for testing if an integer is prime. The result of this theorem is very nice and surprising.
Theorem: Fermat’s Little Theorem.
Let a be an integer and p be a prime, then:
ap ≡ a mod p.
This theorem is often very useful in public-key cryptography. One application is to compute an inverse in a finite field by using arithmetic in finite fields like GF(p) which is done modulo p, hence Fermat’s little theorem is true for all integers a that are elements of GF(p), i.e.:
ap – 1 ≡ 1 mod p.
is still true. Then notice we could rewrite this equation as:
a ⋅ ap – 2 ≡ 1 mod p.
Which as you may notice is the definition of the multiplicative inverse. It gives us a nice way to invert an integer a modulo a prime!
Euler's Theorem
Euler’s theorem is a generalization of Fermat’s little theorem to any integer, that do not necessarily need to be primes. The theorem is as follows:
Theorem: Euler’s Theorem.
Let a and m be integers with gcd(a, m) = 1, then:
aϕ(m) ≡ 1 mod m.
Since it works modulo m, Euler’s theorem works on integer rings ℤm. This may seem a little weird, but lets see an example with small values.
Example: Let m = 12 and a = 5. Then we can use Euler’s Phi Function to find:
ϕ(12) = (22 – 21) ⋅ (31 – 30) = 2 ⋅ 2 = 4.
Then we can use Euler’s theorem:
5ϕ(12) = 54 = 625 ≡ 1 mod 12.
Conclusion
This was a very math-intensive blog post. But these types of discussions are necessary for understanding the security of cryptography. Even more so in public-key cryptography where algorithms are very math-heavy. If you made it through this entire post that is quite impressive, if you didn’t I’m sure you are not reading this, but I will always link back to this post in future discussions, and try to give a brief refersher when necessary.













