What is Cryptology?
The Oxford Dictionary defines Cryptology as: “the study of codes, or the art of writing and solving them”. When some people think of Cryptology people may think of secure website access, bank cards, or more modern “Cryptocurrency”. All of these would be correct, but cryptology is actually a much older business than the examples given.
Many examples of cryptology actuall date back all the way to ancient Egypt who used hieroglyphics. Since then most cultures have used cryptology. For example, the famous Caesar Cipher used in ancient Rome, which will be discussed in a future blog post. Or a more modern example of the Enigma Machine used in World War 2 by Germany.
But as interesting as these old examples are, we will learn how to break them and focus on modern cryptologic methods used today.
Lets have a look at how the field of cryptology is broken up:
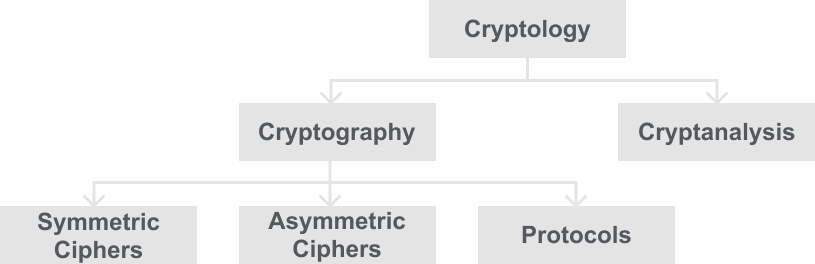
The first thing you may notice is that generally the field is most commonly called “Cryptography” and in fact I may generally call it just cryptography from this point onwards. But Cryptography is just a branch of Cryptology and is further broken up from there. Here is some further information on the two branches of Cryptology:
Cryptography
Cryptography is the science of hiding a message, ie creating the method of hiding a message.
Cryptanalysis
You may think from this that Cryptography is the good guy and Cryptanalysis is the bad guy trying to gain secrets for nefarious reasons. While this is true in some cases, most cryptanalysis is done by researchers and is the basis of how we know cryptosystems created by cryptographers are secure.
Both will be covered in this blog, because one cannot be without the other. In either field you are interested in you need to keep the other in mind.
Lets go back to the diagram and go back over the 3 main splits of Cryptography then:
Symmetric Ciphers
Symmetric Ciphers are algorithms with two parties both with an encryption and decryption method and share a key among them, all cryptography before 1976 is based on this. This does not mean they are not still widespread, and we will learn about the most popular ones, 3DES and AES.
Asymmetric Ciphers
Asymmetric Ciphers or Public Key Algorithms were first used in 1976, by Ron Rivest, Adi Shamir, and Leonard Adleman, who created RSA. Asymmetric ciphers where there are 2 different keys, a private key, and a public key. This will also be covered in RSA and Diffie-Helmann.
Protocols
Protocols are applications of cryptographic algorithms, and more will be talked about in later blogs like message authentication.
Basics/ set-up of a symmetric cipher
It is important to define what our problem is, and what we want to do first. Our problem is that we want to communicate over an “insecure channel”. For example, if two people Alice and Bob wanted to talk to each other on a bench in the park, but someone is sitting between them named Malcom how can Alice and Bob communicate without Malcom understanding what they are saying? We will show this in a diagram:
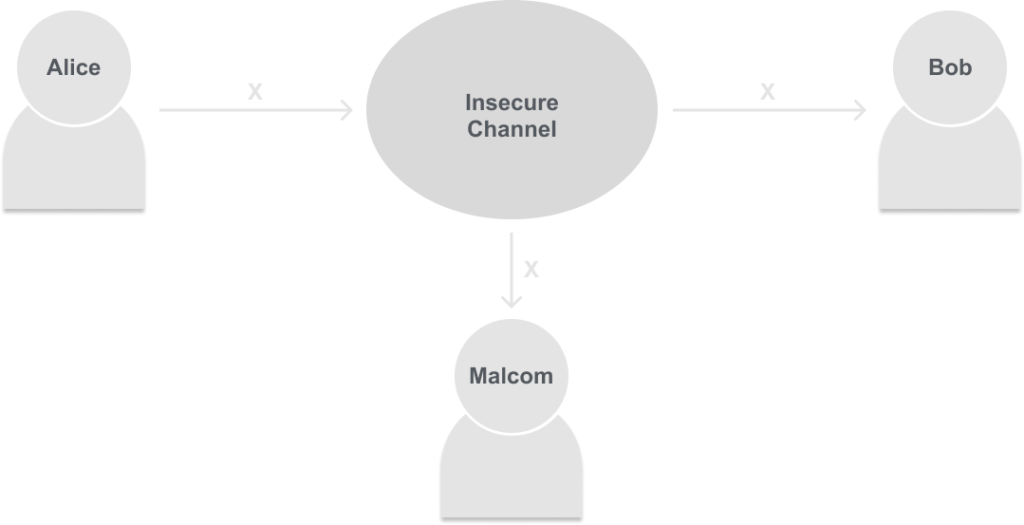
Alice is trying to communicate message ‘X’ to Bob, but since Malcolm is in the middle of them he can also hear message ‘X’ just fine.
Now instead of the nice bench in the park let’s think of the insecure channel as the internet, airwaves, wifi, etc. The diagram works just fine, but we need a way to communicate ‘X’ through the insecure channel in a way that Bob understands but not Malcolm.
In this scenario, Symmetric cryptography offers a solution. Instead of Alice sending the plain message of ‘X’ into the insecure channel, Alice will first encrypt her message producing the ciphertext ‘Y’. Bob then receives ‘Y’, and is able to decrypt the message back into ‘X’. This is shown below:
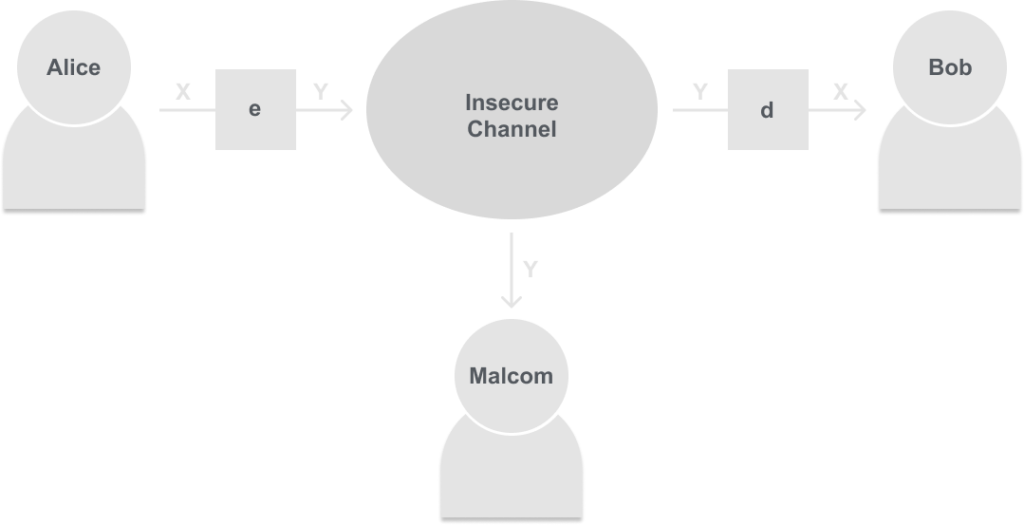
Now instead of Malcolm seeing the message ‘X’ he only sees ‘Y’, which in practice would look like random letters and numbers.
But now here is a question, should Alice and Bob keep it a secret on how to encrypt (e) and decrypt (d)?
No, it may seem counterintuitive that we tell everyone including Malcolm how we are encrypting and decrypting our messages, but it is actually the best way to ensure our methods are secure. In practice, a cryptosystem that you create and think is very secure in practice may be very weak. So if you try to use it and Malcolm is an experienced cryptanalyst he would be able to break your system and read all of your messages.
But you may be thinking to yourself right now, “Well if we told Malcolm how to decrypt he could decrypt Y into X just like Bob”, and you would be correct. In this diagram, it would be a dumb idea frankly. That is why we will introduce a new parameter called a Key, and without it you cannot decrypt or encrypt. So as long as Alice and Bob share this key privately and Malcolm cannot get it, Malcom can never actually decrypt our messages sent through the insecure channel. Here is the diagram for that:
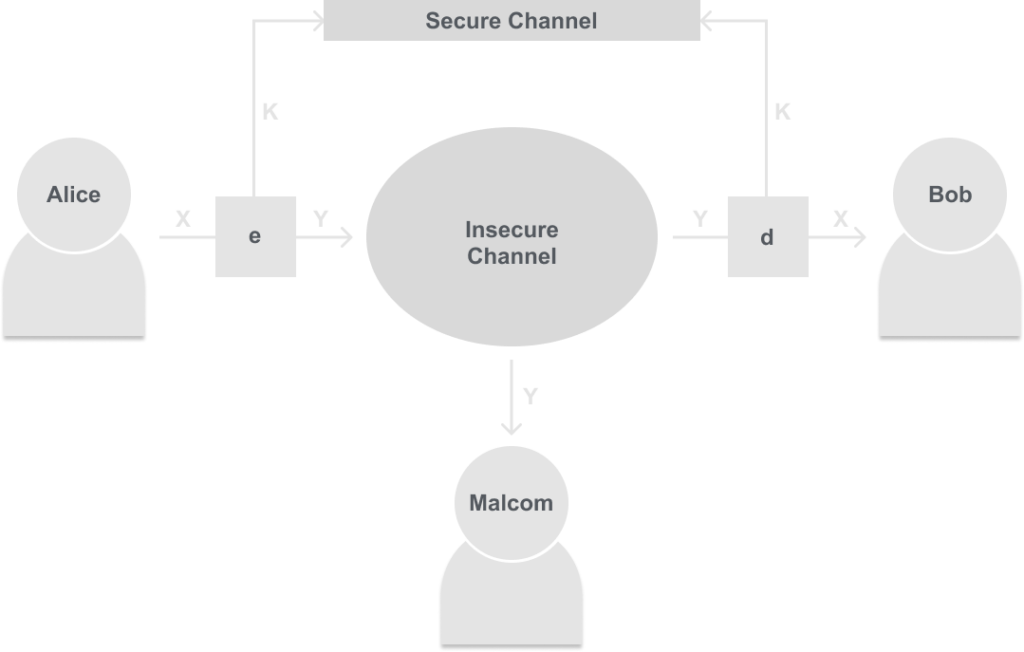
This is the basic diagram that all symmetric ciphers are built from. Some questions you may have are, “Why use the insecure channel if you have the secure channel?” Well mainly convenience, it is much easier to message a friend over the internet than it is to coordinate a in-person meeting to tell them something.
But for this cryptosystem to work we first need this secure channel, which could be an in-person meeting, a letter, etc. We will discuss in later posts how to exchange a key over an insecure channel in the diffie-hellman post. But for now, just think of an in-person meeting.
Notation
X is called the plaintext. This is the message we want to send.
Y is the ciphertext. This is the message we will send through the insecure channel.
e is the notation for the encryption algorithm.
d is the notation for the decryption algorithm, this is also the inverse of e.
k is called the key
|k| is called the key space. This is how many possible keys there are, for now just think the bigger the number the better the system.













