(DES) The Data Encryption Standard [Part 1]

Introduction

The Data Encryption Standard (DES) was proposed in the early 1970s by IBM, who based the design of the cipher on an earlier design by Horst Feistel. The cipher was created as a request by the United States National Bureau of Standards (NBS) which is the modern-day National Institute of Standards and Technology (NIST).

In 1976 with consultation from the National Security Agency (NSA), the NBS selected the cipher that we know today as DES. The DES quickly became adopted by companies and groups. This has meant that DES is one of the best-studied ciphers in the world, with many academic bodies and governments trying to break DES. This is because of some controversies surrounding the groups who created the cipher which I will get into later.

As of 2023, because of found insecurities of DES which will be discused in this post. The DES is no longer allowed to be used for encryption.

Block Ciphers

This is our first introduction to block ciphers, so it is important to know how to make a secure block cipher. According to the American Mathematician Claude Shannon, there are two primitive operations with which strong encryption algorithms can be built, those are:

Confusion is an encryption operation where the relationship between the plaintext and cipher text is obscured. For example, is a substitution table from our substitution cipher.
Diffusion is an encryption operation where the influence of one change plaintext bit is spread out over many ciphertext bits. The goal is to confuse the statistical properties of the plaintext. This is usually done with a permutation, which scrambles the bits in a block.

Most ciphers that we looked at before like the substitution cipher or the German Enigma machine only use confusion, which is why they are considered weak ciphers. But we can get around this by repeating our two operations confusion and diffusion many times to build a strong cipher. This idea was proposed by Claude Shannon, which he called product ciphers and all of today’s block ciphers are product ciphers that consist of rounds of repeatedly applying confusion and diffusion like below:

Feistel Network

Many of today’s ciphers are Feistel ciphers. Though there are many modern ciphers that are Feistel ciphers, not all are. For example, the next big cipher we will discuss AES is not a Feistel cipher.

A Feistel cipher takes your plaintext x and a key that we call a subkey and repeats encryption rounds multiple times. These encryption rounds will include confusion and diffusion so that we have a secure cipher. One advantage of Feistel ciphers is that encryption and decryption are almost the same operation. Decryption only requires that we reverse the key schedule (don’t worry if you don’t recognize that part, continue reading and you will understand).

Overview of DES

The DES is a cipher that encrypts blocks of length 64 bits with a key of size 56 bits, check the figure below:

DES is a symmetric cipher, therefore the same key is used for encryption and decryption. DES is a Feistel cipher, meaning that each plaintext block is encrypted in 16 rounds which each do identical operations. The diagram below will show the round structure of DES.

It is important to note that DES has a new feature not discussed in past posts which is that every round doesn’t use the same key, instead each round uses a subkey, which is all derived from the main key. This is an important part of DES and block ciphers, that is why I will not try to squeeze that in here and will go into greater depth of the subkeys and key schedule in DES part 2.

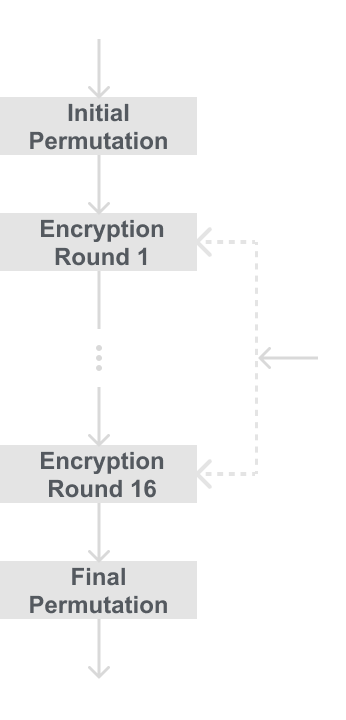
Algorithm

After the Initial Permutation (IP), the 64 plaintext bits are split into two halves a left (L) and a right (R), these two halves are the input into the Feistel cipher which consists of 16 rounds. The right half is fed into another f function, then the output of that f function is XORed with the left half. Then finally the Left and Right halves are swapped, fed into the next round, and repeated until all 16 are done. After the 16 rounds the Left and Right halves are combined into a 64-bit ciphertext and permuted once more in the Final Permutation(FP). Each round uses a subkey, which is derived from the 56-bit main key.

That was a lot of reading, I have a diagram below to hopefully make that make more sense:

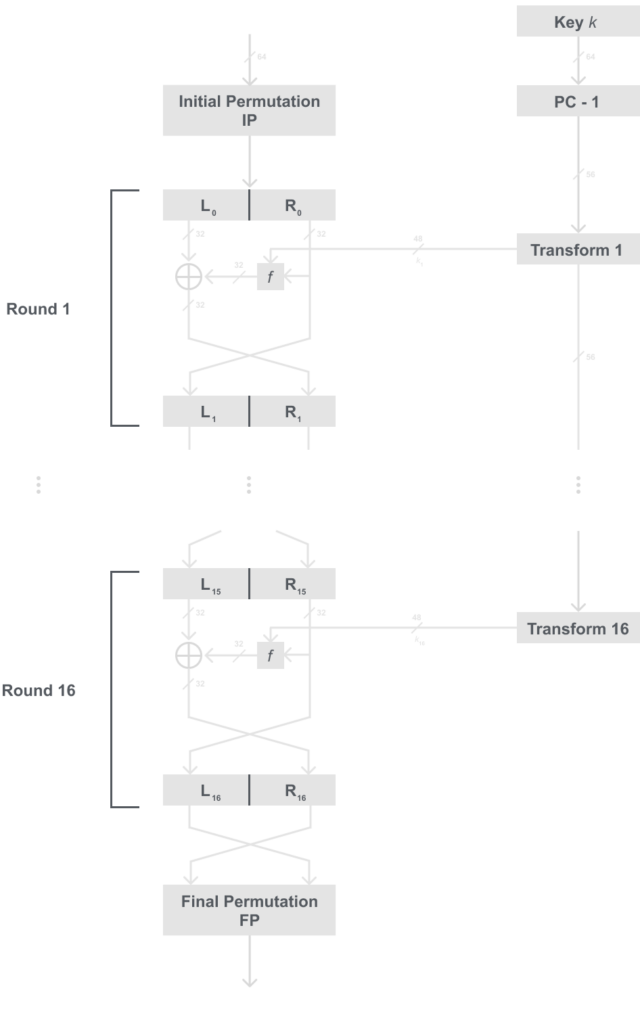
Q: Which half of each block is actually being encrypted?
A: Most people’s first guess is that the right half is the half being encrypted because that is the half being put through the f function. But when you look at it longer, it is actually the left half being encrypted with the XOR, and the right half just falls through and becomes the next left half.

The reason I went over stream ciphers was so you would have a better grasp of the XOR in DES. We learned from stream ciphers when a cryptosystem uses XOR it is important that the key is pseudo-random, and using a key the same size of the message helps security. We know that the OTP is impractical in reality, but we can use that idea and modify it for DES.

The output of the f function can be viewed as the pseudo-random key stream we used in stream ciphers and the OTP. To further explain this connection take a look at this diagram which is laid out like our stream cipher diagram:

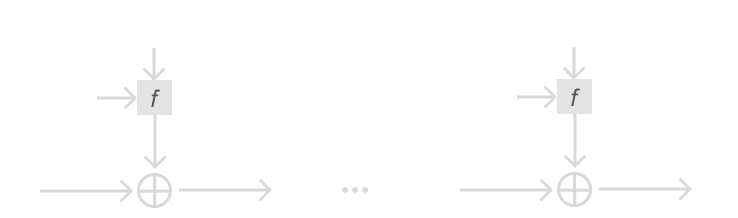
DES Internals

It may seem like each time we go deeper into the DES algorithm we find new things we don’t know yet. The main thing you are probably asking is “What is the f function?”, well I am happy to say that the f function is our last for part 1, and ill break it into sections below.

Initial and Final Permutation

As in the diagram below, the Initial and Final permutations are bitwise permutations. If you are unfamiliar with what that means, a bitwise permutation is like connecting wires. This like most other cryptosystems makes the most sense in hardware as this is done literally with wires.

Interestingly the reason for the Initial and Final permutation is not really known, one theory is that it was necessary for the hardware at the time. But the Initial and Final permutations do not add to the security of the cipher.

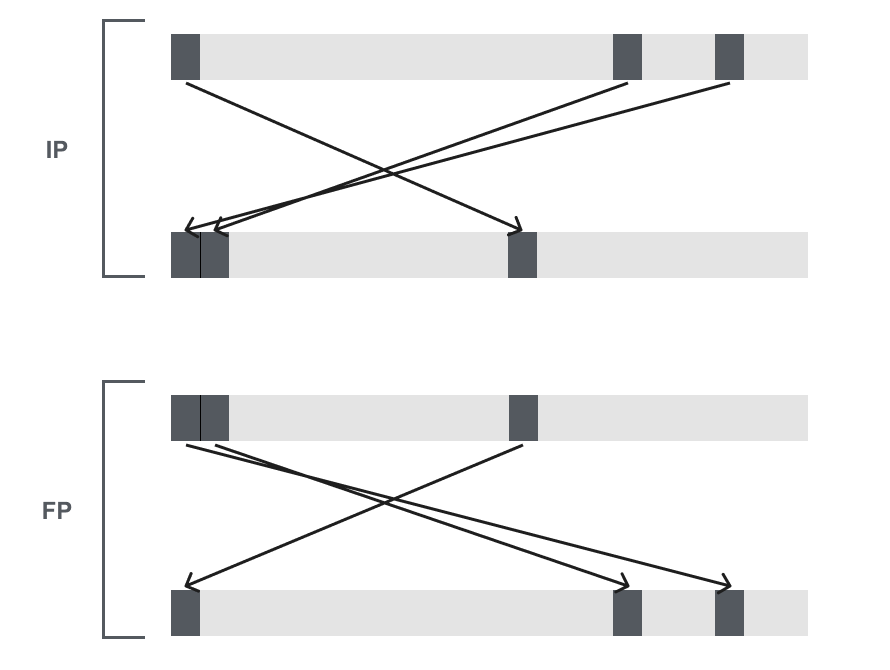
The details of the IP and FP are given in the table below. It is to be read from left to right, top to bottom. The table indicates the input bit 58 is mapped to output position 1, input bit 50 is mapped to the second output, and so on. Notice that FP performs the inverse of IP.

IP

58	50	42	34	26	18	10	2
60	52	44	36	28	20	12	4
62	54	46	38	30	22	14	6
64	56	48	40	32	24	16	8
57	49	41	33	25	17	9	1
59	51	43	35	27	19	11	3
61	53	45	37	29	21	13	5
63	55	47	39	31	23	15	7

FP

40	8	48	16	56	24	64	32
39	7	47	15	55	23	63	31
38	6	46	14	54	22	62	30
37	5	45	13	53	21	61	29
36	4	44	12	52	20	60	28
35	3	43	11	51	19	59	27
34	2	42	10	50	18	58	26
33	1	41	9	49	17	57	25

The f -Function

The f-function is crucial to the security of DES. Looking back to our diagram of the internals of an encryption round i, the f-function takes the right half R_{i – 1} of the output of the previous round and the current subkey k_i as an input. Then as mentioned before, the output of the f-function is then XORed with the L_{i – 1} half.

Now we need to actually break down what is inside the f-function, refer to the diagram below of the f-function, and then I will break down each part:

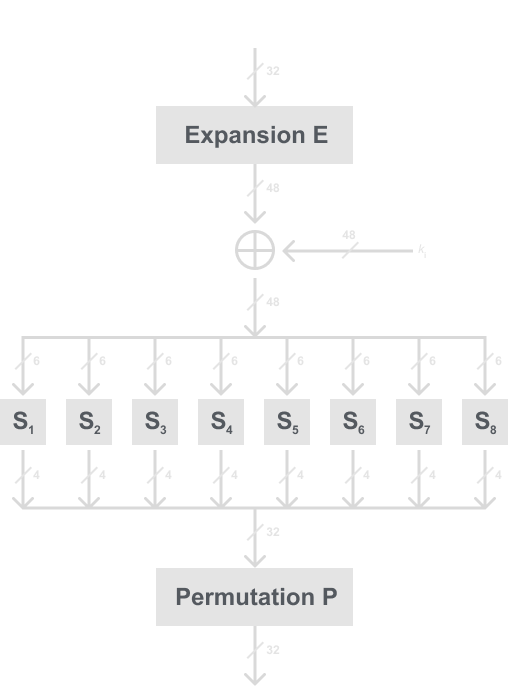
I do recognize that each time we keep going into the internals of DES there is something else we need to learn about. But I swear (for at least this part) that these are the last things we need to learn for the encryption algorithm.

Expansion function

The first part of the f-function is the expansion function. We take our right half, which is 32 bits, and expand it to 48 bits. You may notice by the diagram below that this is similar to the initial and final permutation, but this adds to the security of DES by supplying diffusion to the algorithm.

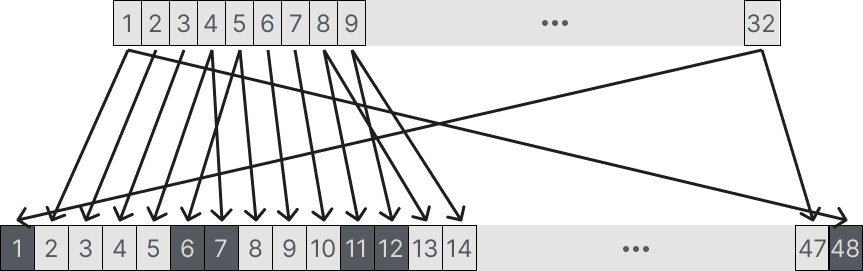
Recall that DES is based on Shannon’s theory of a secure cipher, this we need confusion and diffusion. Then notice that this gives DES diffusion because each bit from our 32-bit input if changed now has a 50/50 chance of changing in 2 places. As seen in the diagram exactly 16 of the 32 inputs appear twice in the output.

Below is the permutation table for E:

Expansion permutation E

32	1	2	3	4	5
4	5	6	7	8	9
8	9	10	11	12	13
12	13	14	15	16	17
16	17	18	19	20	21
20	21	22	23	24	25
24	25	26	27	28	29
28	29	30	31	32	1

The 48-bit result of the expansion is then XORed with the rounds subkey. Then we move on to the heart of DES, the s-boxes.

The S-boxes

After the 32-bits are expanded into 48-bits and XORed with the subkey, the result of that is split up into 8 6-bit blocks which are all fed into 8 different substitution boxes, which are referred to as s-boxes. Each s-box is a lookup table that takes 6 bits and outputs 4 bits.

Each s-box is a table with 4 rows and 16 columns, larger tables would have been more secure but this was probably a limitation of the time. Each s-box table will be labeled below, so note that each s-box is different.

The tables are read like in the example below: the most significant bit (MSB) and least significant bit (LSB) (es. the first and last bit) of each 6-bit input selects the row and the four inner bits select the column. In each table below the integers 0,1, …, 15 are the decimal notation of a 4-bit value.

Ex: Take a possible input b = (100101)₂, we take the MSB and LSB (the first and last bit), 11₂ = 3 which indicates the row. Then the inner 4 bits, 0010₂ = 2 indicate the column.

For this example we input this into s-box 1, thus our output will be in row 3 column 2. The output is 8 = 1000₂.

S-box S₁

S₁	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	14	4	13	1	2	15	11	8	3	10	6	12	5	9	0	7
1	0	15	7	4	14	2	13	1	10	6	12	11	9	5	3	8
2	4	1	14	8	13	6	2	11	15	12	9	7	3	10	5	0
3	15	12	8	2	4	9	1	7	5	11	3	14	10	0	6	13

S-box S₂

S₂	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	15	1	8	14	6	11	3	4	9	7	2	13	12	0	5	10
1	3	13	4	7	15	2	8	14	12	0	1	10	6	9	11	5
2	0	14	7	11	10	4	13	1	5	8	12	6	9	3	2	15
3	13	8	10	1	3	15	4	2	11	6	7	12	0	5	14	9

S-box S₃

S₃	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	10	0	9	14	6	3	15	5	1	13	12	7	11	4	2	8
1	13	7	0	9	3	4	6	10	2	8	5	14	12	11	15	1
2	13	6	4	9	8	15	3	0	11	1	2	12	5	10	14	7
3	1	10	13	0	6	9	8	7	4	15	14	3	11	5	2	12

S-box S₄

S₄	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	7	13	14	3	0	6	9	10	1	2	8	5	11	12	4	15
1	13	8	11	5	6	15	0	3	4	7	2	12	1	10	14	9
2	10	6	9	0	12	11	7	13	15	1	3	14	5	2	8	4
3	3	15	0	6	10	1	13	8	9	4	5	11	12	7	2	14

S-box S₅

S₅	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	2	12	4	1	7	10	11	6	8	5	3	15	13	0	14	9
1	14	11	2	12	4	7	13	1	5	0	15	10	3	9	8	6
2	4	2	1	11	10	13	7	8	15	9	12	5	6	3	0	14
3	11	8	12	7	1	14	2	13	6	15	0	9	10	4	5	3

S-box S₆

S₆	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	12	1	10	15	9	2	6	8	0	13	3	4	14	7	5	11
1	10	15	4	2	7	12	9	5	6	1	13	14	0	11	3	8
2	9	14	15	5	2	8	12	3	7	0	4	10	1	13	11	6
3	4	3	2	12	9	5	15	10	11	14	1	7	6	0	8	13

S-box S₇

S₇	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	4	11	2	14	15	0	8	13	3	12	9	7	5	10	6	1
1	13	0	11	7	4	9	1	10	14	3	5	12	2	15	8	6
2	1	4	11	13	12	3	7	14	10	15	6	8	0	5	9	2
3	6	11	13	8	1	4	10	7	9	5	0	15	14	2	3	12

S-box S₈

S₈	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	13	2	8	4	6	15	11	1	10	9	3	14	5	0	12	7
1	1	15	13	8	10	3	7	4	12	5	6	11	0	14	9	2
2	7	11	4	1	9	12	14	2	0	6	10	13	15	3	5	8
3	2	1	14	7	4	10	8	13	15	12	9	0	3	5	6	11

You may wonder if there is some equation to compute these instead of using these lookup tables, and the answer is actually no.

The S-boxes are the heart of DES in terms of the cryptographic strength of DES. They are the only non-linear element of the algorithm and they provide the confusion from Shannons theory. Even though the entire DES algorithm was revealed, the motivation behind the s-boxes wasn’t revealed. This gave rise to speculation and theories of a conspiracy of a secret back door or a weakness that could be exploited by the NSA, who consulted IBM when creating DES.

However, we now know that the S-boxes were designed according to a list of criteria which I will not add here because this post is already long. But the criteria basically ensure that the S-boxes provide non-linearity to the algorithm. Without nonlinearity, an attacker could express the DES input and outputs as a system of linear equations and solve for the unknown key bits. If you want more information about this attack make sure to read my Stream Ciphers and Linear Feedback Shift Registers post where we use this attack to break stream ciphers using LFSRs. This is the same attack and was coined differential cryptanalysis. Interestingly this attack was first discovered in the research community in 1990. But the IBM team revealed they already knew of the attack 16 years prior, thus why they designed DES with non-linearity in mind.

Permutation function

This is the last part of the f-function and the most simple part. The permutation function takes the 32-bit output of the s-boxes and permutes bitwise according to the P permutation table given below. This is very similar to the Initial and Final permutation, but unlike those, this actually adds to the security by adding diffusion. This is because it permutes the bits in such a way that it will affect the inputs of the next rounds of s-boxes.

The diffusion of the permutation ensures that every bit at the end of the fifth round is a function of every plaintext bit and every key bit.

Permutation P within f-function

16	7	20	21	29	12	28	17
1	15	23	26	5	18	31	10
2	8	24	14	32	27	3	9
19	13	30	6	22	11	4	25

This is the end of Part 1, but make sure to read Part 2 where I will go into the DES key schedule and decryption.

Part 2 will also include the C++ code implementation of the DES encryption algorithm.

(DES) The Data Encryption Standard [Part 1]

Table of Contents

Introduction