Brief History
In 1997, the National Institute of Standards and Technology (NIST) called to replace the DES. By this time DES was considered dying because of its small key space discussed in the DES post. This was unlike when DES was designed because the selection of the AES algorithm was an open-source process. By 1998 only 15 algorithms were submitted to the competition and by 1999 that list was reduced to the 5 AES finalists. Among the finalists were well-known cipher creators like IBM the creator of DES. But on October 2nd, 2000, Rijndael was chosen and known today as AES.
The Rijndael cipher was created by two young Belgian cryptographers, Joan Daeman and Vincent Rijmen.
I would also like to mention a fun fact about AES, which is by this time many intelligence agencies like NSA, MI6, FSB, etc would use their own cipher. But in 2003 the US National Security Agency (NSA) announced that it allows AES to encrypt classified documents up to the level SECRET for all key lengths, and up to the TOP SECRET level for key lengths of either 192 or 256 bits. Therefore it is a safe bet to assume that the AES is a very secure algorithm.
Overview of AES
The AES is a block cipher that encrypts 128 bits at a time. Unlike the DES which encrypted 64 bits at a time. Also different from the DES, one requirement for algorithms submitted for the AES competition was that it has modular key sizes. Therefore the AES standard is capable of using 128/ 192/ 256 bit-sized keys. The larger the key, the more secure AES.
Recall that block ciphers also use two primary techniques confusion and diffusion to ensure that the cipher is secure, and these techniques are also repeated in multiple rounds. This is discussed more in the post about DES, so if you are unfamiliar make sure to read that and then come back here.
As mentioned before, AES has three different key lengths. The number of rounds is determined by the length of the key chosen according to the table below:
| Key Length | # of rounds |
| 128 | 10 |
| 192 | 12 |
| 256 | 14 |
In contrast to DES, AES is not a Feistel network. So unlike DES which encrypts half a block at a time, the AES encrypts all 128-bit blocks at a time. That is why it can use fewer rounds while being more secure than DES.
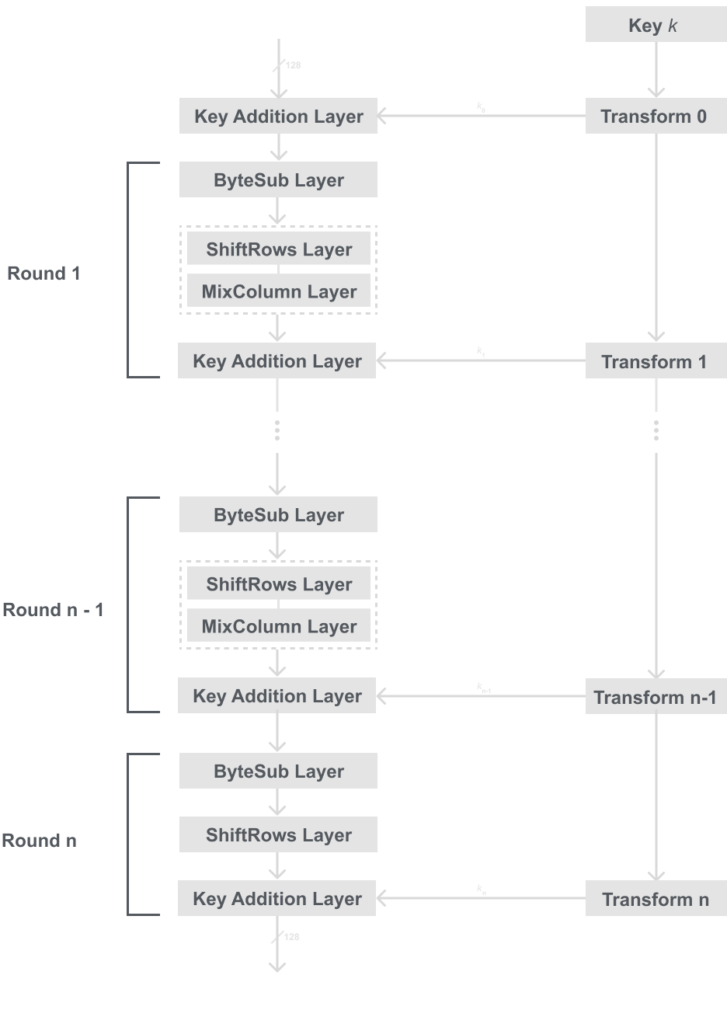
AES consists of layers that we pass our data through. Each layer manipulates all 128 bits of the data, and these layers introduce either confusion or diffusion to our algorithm.
AES Layers
Key Addition Layer: A 128-bit round key/ subkey which like DES is derived from a main key in the key schedule, is XORed with the data.
Byte Substitution Layer (S-Box): Each element of the state in transformed using a single lookup table derived with mathematical properties. This introduces confusion to the algorithm.
Diffusion Layer: This layer consists of two sub layers and provides diffusion over all the states bits:
- ShiftRows: Permutes the data on a byte level
- MixColumn: Matrix operation which mixes blocks of four bytes.
Below is a diagram of how the layers are ordered:
Now that we know the basic structure of AES, we now have to answer what happens inside these layers. Therefore it will first be good to know that in AES we operate on bytes where 1 byte = 8 bits.
Below is a model showing the insides of the AES layers, this will still seem abstract, but later when we describe the layers more referring to this model should help:
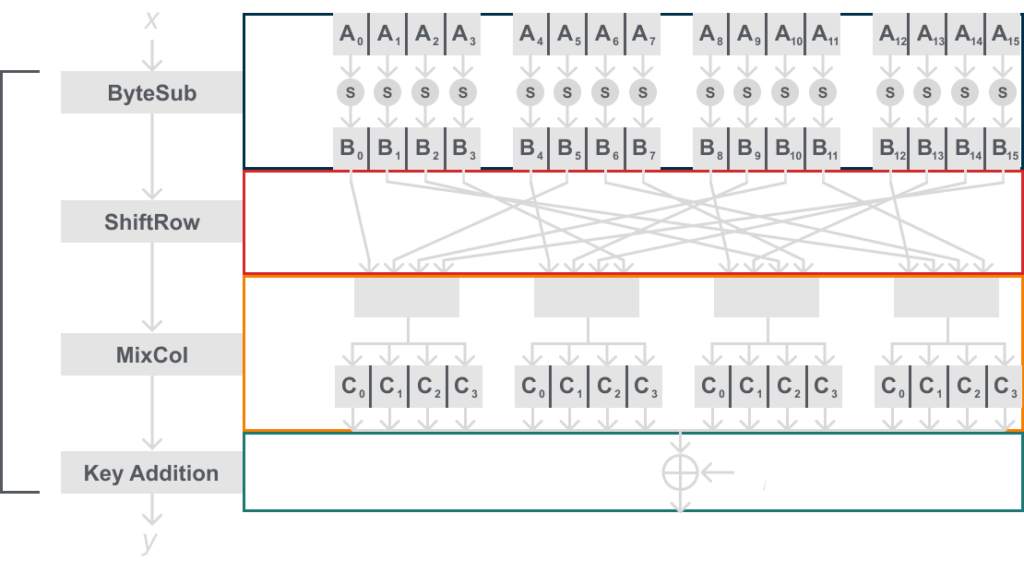
I know this may seem like a lot if you’re not used to it, but this really isn’t bad once we learn more about what is happening within ByteSub, ShiftRow, and MixCol.
But before we get into those in detail it is important to state that it is helpful to imagine the 16 bytes arranged in a 4×4 byte matrix, you can see how we show the matrix below:

ByteSub
Byte Substitution or ByteSub is the first layer in each round. The ByteSub layer is a row of parallel S-Boxes, each that takes an input of 1 byte and output 1 byte. Note that, unlike DES, all 16 S-Boxes are identical. In the layer, each state byte Ai is replaced or substituted by another Bi byte.
We can represent that as: S(Ai) = Bi.
The S-Box is the non-linear element of AES, this is to make sure an attack called differential cryptanalysis is ineffective against AES. The S-Box has a special mathematical derivation and can be computed during encryption and decryption. But typically in software, the S-Box is just a lookup table with fixes entries. You can see the S-Box table below:
| Ai | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 63 | 7c | 77 | 7b | f2 | 6b | 6f | c5 | 30 | 01 | 67 | 2b | fe | d7 | ab | 76 |
| 1 | ca | 82 | c9 | 7d | fa | 59 | 47 | f0 | ad | d4 | a2 | af | 9c | a4 | 72 | c0 |
| 2 | b7 | fd | 93 | 26 | 36 | 3f | f7 | cc | 34 | a5 | e5 | f1 | 71 | d8 | 31 | 15 |
| 3 | 04 | c7 | 23 | c3 | 18 | 96 | 05 | 9a | 07 | 12 | 80 | e2 | eb | 27 | b2 | 75 |
| 4 | 09 | 83 | 2c | 1a | 1b | 6e | 5a | a0 | 52 | 3b | d6 | b3 | 29 | e3 | 2f | 84 |
| 5 | 53 | d1 | 00 | ed | 20 | fc | b1 | 5b | 6a | cb | be | 39 | 4a | 4c | 58 | cf |
| 6 | d0 | ef | aa | fb | 43 | 4d | 33 | 85 | 45 | f9 | 02 | 7f | 50 | 3c | 9f | a8 |
| 7 | 51 | a3 | 40 | 8f | 92 | 9d | 38 | f5 | bc | b6 | da | 21 | 10 | ff | f3 | d2 |
| 8 | cd | 0c | 13 | ec | 5f | 97 | 44 | 17 | c4 | a7 | 7e | 3d | 64 | 5d | 19 | 73 |
| 9 | 60 | 81 | 4f | dc | 22 | 2a | 90 | 88 | 46 | ee | b8 | 14 | de | 5e | 0b | db |
| A | e0 | 32 | 3a | 0a | 49 | 06 | 24 | 5c | c2 | d3 | ac | 62 | 91 | 95 | e4 | 79 |
| B | e7 | c8 | 37 | 6d | 8d | d5 | 4e | a9 | 6c | 56 | f4 | ea | 65 | 7a | ae | 08 |
| C | ba | 78 | 25 | 2e | 1c | a6 | b4 | c6 | e8 | dd | 74 | 1f | 4b | bd | 8b | 8a |
| D | 70 | 3e | b5 | 66 | 48 | 03 | f6 | 0e | 61 | 35 | 57 | b9 | 86 | c1 | 1d | 9e |
| E | e1 | f8 | 98 | 11 | 69 | d9 | 8e | 94 | 9b | 1e | 87 | e9 | ce | 55 | 28 | df |
| F | 8c | a1 | 89 | 0d | bf | e6 | 42 | 68 | 41 | 99 | 2d | 0f | b0 | 54 | bb | 16 |
There is a special way to read this lookup table just like DES. Recall that the input to the S-Box is 1 byte= 8 bits. We use the first 4 bits for the row, and the last 4 bits for the column.
Check the example below to see how we do this:
Example
Let Ai = 5316 (This is in hexadecimal)
We take the ‘516‘ to find the row and the ‘316‘ for the column. So we get this:
S(Ai = 53) = Bi = ED16 = 1110 11012.
Mathematical Description of the S-Box
I mentioned this before, but unlike DES the S-Box in AES has a mathematical description and can be computed. Note that if you want to implement AES in software it makes more sense to just save it as a 2darray. But if you are implementing it in hardware computing it would be better.
The AES S-Box can be viewed as a two-step mathematical transformation:

If you do not recognize GF(28), this is a Galoid Field, and I discussed it in the last post Introduction to Galoid Fields for AES. This will give you a better idea of this mathematical description and is highly encouraged to read. For each input byte Ai, the inverse is computed Bi‘ = A i-1 and is reduced using the AES polynomial discussed in the last post.
In the second part, each byte Bi‘ is multiplied by a constant bit matrix and then added with a constant 8-bit vector. You can see the mathematical formula below:
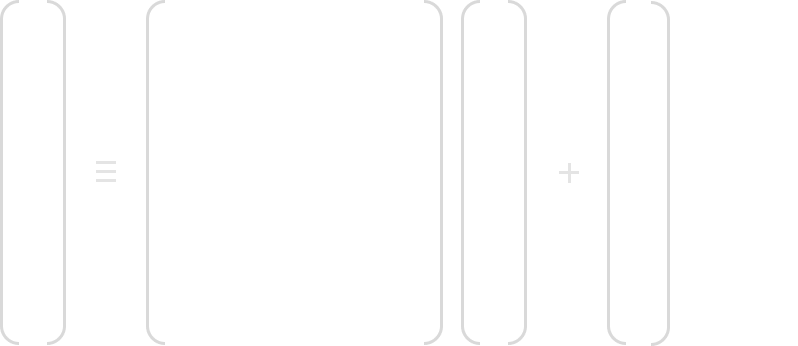
Example
Let Ai = 5316 = 0101 00112.
Then calculate the inverse A i-1 = Bi‘ =(CA16) = 1100 10102.
Now break Bi‘ =( b0‘ b1‘ b2‘ b3‘ b4‘ b5‘ b6‘ b7‘ ), multiply using the bit matrix, then add the 8-bit vector and reduce modulo 2. This gives our result:
Bi = (1110 11012) = ED16
This could probably seem like a lot, but thankfully this is a fixed table, meaning we only have to compute this once. In fact, we don’t have to compute it at all because someone already did that for us so we can just copy and paste.
This was really just for people who are like me and want to know every part of an algorithm or for people who want to implement this in hardware.
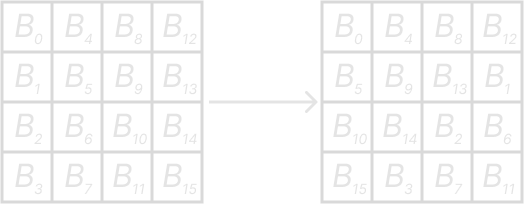
ShiftRow
Looking back at our diagram the next layer can seem a little wild and random like the permutations in DES. But it is actually very systematic if we look at our data state as a 4×4 matrix.
In the ShiftRow layer we shift each row cylindrically, meaning data rotates over. The rows are shifted by these rules:
- First row is not changed
- Second row is shifted 3 times to the right
- Third row is shifted 2 times to the right
- Fourth row is shifted 1 time to the right
Here is a diagram to better show how this works:
MixCol
The Mix Column or MixCol layer is the largest provider of diffusion in AES. The combination of the ShiftRow and MixCol layers makes it possible after only 3 rounds that every byte of the state matrix is determined by the 16 plaintext bytes.
In MixCol layer each 4-byte colum is considered a vector and multiplicated by a fixed 4×4 matrix. This matrix has constant values in which multiplication and addition is done in GF(28). Below is the mathematical formula, and the 4×4 constant matrix:
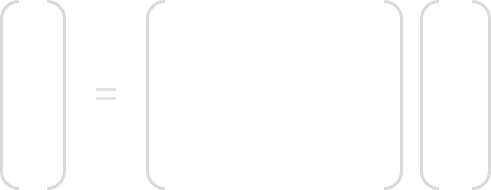
Here is an example of how we would compute C0
Example
Note that these numbers 01, 02, and 03 are hexdecimal numbers, therefore these numbers have bit definitions for GF(28) polynomials. Therefore we must compute these in GF(28) meaning we need to follow addition and multiplication rules in GF(28). We went over that in Introduction to Galois Fields for AES. So if you are interested in learning that make sure to read that.
Key Addition
The two inputs from our diagram are the current 16-byte state matrix and the subkey. The two inputes are combined with the bitwise XOR operation. Recall that XOR is also the same as addition in GF(2).
The subkey is derived in the key schedule that we will discuss in part 2.
Conclusion
You may notice that we didn’t quite get to everything in this post. I split AES into 2 parts, and in part 2 we will go over the Key Schedule, AES decryption, code implementation, and attacks. So make sure to look out for that, or follow this link here: [LINK]













